Mister Exam
Other calculators
- Taylor Series Step by Step
- Fourier series step by step
- Differential equations Step by Step
- Product of series
-
How to use it?
- Sum of series:
-
n^2*sin(5/(3^n))
- x^n/(1-x^n)
-
762.5*(0.525*0.475)^n
-
1,04348*10^7
-
Identical expressions
- u(one . seven *n)*(sin(four * zero . seventy-eight (zero . one hundred and eighty-four - one . seven *n)))/ four * zero . seventy-eight (zero . one hundred and eighty-four - one . seven *n)
- u(1.007 multiply by n) multiply by ( sinus of (4 multiply by 0.78(0.184 minus 1.007 multiply by n))) divide by 4 multiply by 0.78(0.184 minus 1.007 multiply by n)
- u(one . seven multiply by n) multiply by ( sinus of (four multiply by zero . seventy minus eight (zero . one hundred and eighty minus four minus one . seven multiply by n))) divide by four multiply by zero . seventy minus eight (zero . one hundred and eighty minus four minus one . seven multiply by n)
- u(1.007n)(sin(40.78(0.184-1.007n)))/40.78(0.184-1.007n)
- u1.007nsin40.780.184-1.007n/40.780.184-1.007n
- u(1.007*n)*(sin(4*0.78(0.184-1.007*n))) divide by 4*0.78(0.184-1.007*n)
-
Similar expressions
- u(1.007*n)*(sin(4*0.78(0.184-1.007*n)))/4*0.78(0.184+1.007*n)
- u(1.007*n)*(sin(4*0.78(0.184+1.007*n)))/4*0.78(0.184-1.007*n)
Sum of series u(1.007*n)*(sin(4*0.78(0.184-1.007*n)))/4*0.78(0.184-1.007*n)
The solution
You have entered
[src]
15
_____
\ `
\ 1007*n /39*4 / 23 1007*n\\
\ u*------*sin|----*|--- - ------||
\ 1000 \ 50 \125 1000 //
) ---------------------------------*39
/ 4 / 23 1007*n\
/ ------------------------------------*|--- - ------|
/ 50 \125 1000 /
/____,
n = 0
$$\sum_{n=0}^{15} \frac{39 \frac{\frac{1007 n}{1000} u \sin{\left(\frac{4 \cdot 39}{50} \left(\frac{23}{125} - \frac{1007 n}{1000}\right) \right)}}{4}}{50} \left(\frac{23}{125} - \frac{1007 n}{1000}\right)$$
Sum(((((u*(1007*n/1000))*sin((39*4/50)*(23/125 - 1007*n/1000)))/4)*39/50)*(23/125 - 1007*n/1000), (n, 0, 15))
The answer
[src]
/ /503373\ /424827\ /346281\ /271323\ /581919\ /53547\ /114231\ /110643\ /76752\ /192777\ /189189\ /37479\ /32097\ /4641\ /7137\\
| 167791*sin|------| 119823*sin|------| 79911*sin|------| 48699*sin|------| 44763*sin|------| 9611*sin|-----| 8787*sin|------| 8511*sin|------| 7872*sin|-----| 4943*sin|------| 4851*sin|------| 1922*sin|-----| 823*sin|-----| 714*sin|----| 183*sin|----||
| \12500 / \12500 / \12500 / \ 6250 / \12500 / \ 2500/ \ 6250 / \12500 / \ 3125/ \ 6250 / \12500 / \ 3125/ \12500/ \125 / \1250/|
-39273*u*|- ------------------ - ------------------ - ----------------- - ----------------- - ----------------- - --------------- - ---------------- - ---------------- - --------------- - ---------------- - ---------------- - --------------- - -------------- - ------------- - -------------|
\ 1000 1000 1000 250 200 200 250 1000 125 50 200 125 1000 5 50 /
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
200000
$$- \frac{39273 u \left(- \frac{44763 \sin{\left(\frac{581919}{12500} \right)}}{200} - \frac{167791 \sin{\left(\frac{503373}{12500} \right)}}{1000} - \frac{119823 \sin{\left(\frac{424827}{12500} \right)}}{1000} - \frac{79911 \sin{\left(\frac{346281}{12500} \right)}}{1000} - \frac{9611 \sin{\left(\frac{53547}{2500} \right)}}{200} - \frac{4851 \sin{\left(\frac{189189}{12500} \right)}}{200} - \frac{8511 \sin{\left(\frac{110643}{12500} \right)}}{1000} - \frac{823 \sin{\left(\frac{32097}{12500} \right)}}{1000} - \frac{183 \sin{\left(\frac{7137}{1250} \right)}}{50} - \frac{1922 \sin{\left(\frac{37479}{3125} \right)}}{125} - \frac{8787 \sin{\left(\frac{114231}{6250} \right)}}{250} - \frac{7872 \sin{\left(\frac{76752}{3125} \right)}}{125} - \frac{4943 \sin{\left(\frac{192777}{6250} \right)}}{50} - \frac{714 \sin{\left(\frac{4641}{125} \right)}}{5} - \frac{48699 \sin{\left(\frac{271323}{6250} \right)}}{250}\right)}{200000}$$
-39273*u*(-167791*sin(503373/12500)/1000 - 119823*sin(424827/12500)/1000 - 79911*sin(346281/12500)/1000 - 48699*sin(271323/6250)/250 - 44763*sin(581919/12500)/200 - 9611*sin(53547/2500)/200 - 8787*sin(114231/6250)/250 - 8511*sin(110643/12500)/1000 - 7872*sin(76752/3125)/125 - 4943*sin(192777/6250)/50 - 4851*sin(189189/12500)/200 - 1922*sin(37479/3125)/125 - 823*sin(32097/12500)/1000 - 714*sin(4641/125)/5 - 183*sin(7137/1250)/50)/200000
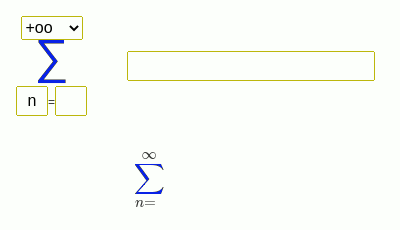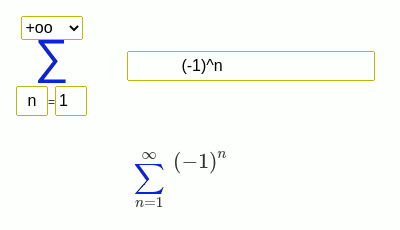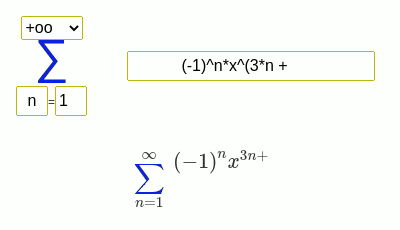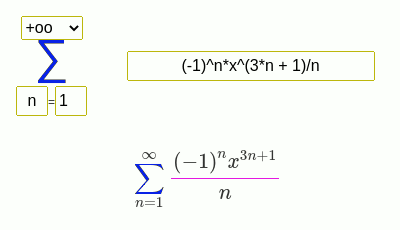
Examples of finding the sum of a series
- The Sum of the Power Series
x^n/n
(x-1)^n
- Factorial
1/2^(n!)
n^2/n!
x^n/n!
k!/(n!*(n+k)!)
- Flint Hills Series
csc(n)^2/n^3
- Basel problem
1/n^2
1/n^4
1/n^6
- Harmonic series
1/n
- Grandi's series
(-1)^n
- Alternating series
(-1)^(n + 1)/n
(n + 2)*(-1)^(n - 1)
(3*n - 1)/(-5)^n
(-1)^(n - 1)*n/(6*n - 5)
- Newton–Mercator series
(-1)^(n + 1)/n*x^n
- Exam the series for convergence
(3*n - 1)/(-5)^n