How do you 1/(x^3+1) in partial fractions?
The solution
Fraction decomposition
[src]
1/(3*(1 + x)) - (-2 + x)/(3*(1 + x^2 - x))
$$- \frac{x - 2}{3 \left(x^{2} - x + 1\right)} + \frac{1}{3 \left(x + 1\right)}$$
1 -2 + x
--------- - --------------
3*(1 + x) / 2 \
3*\1 + x - x/
Combinatorics
[src]
1
--------------------
/ 2 \
(1 + x)*\1 + x - x/
$$\frac{1}{\left(x + 1\right) \left(x^{2} - x + 1\right)}$$
1/((1 + x)*(1 + x^2 - x))

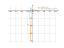 1/(x^3+1)
1/(x^3+1)
 1/(x^3+1)
1/(x^3+1)