Mister Exam
Other calculators:
-
How to use it?
- Limit of the function:
-
Limit of (1+3*x)^(5/x)
-
Limit of e^(1+3*x)*(-1+x)
-
Limit of x*sin(2*x)/3
-
Limit of ((3+n)/(5+n))^(4+n)
- Graphing y =:
- x^2-x^4
- Integral of d{x}:
-
x^2-x^4
- Factor polynomial:
- x^2-x^4
-
Identical expressions
- x^ two -x^ four
- x squared minus x to the power of 4
- x to the power of two minus x to the power of four
- x2-x4
- x²-x⁴
- x to the power of 2-x to the power of 4
-
Similar expressions
- x^2+x^4
Limit of the function x^2-x^4
The solution
You have entered
[src]
/ 2 4\ lim \x - x / x->1+
$$\lim_{x \to 1^+}\left(- x^{4} + x^{2}\right)$$
Limit(x^2 - x^4, x, 1)
Lopital's rule
There is no sense to apply Lopital's rule to this function since there is no indeterminateness of 0/0 or oo/oo type
The graph
One‐sided limits
[src]
/ 2 4\ lim \x - x / x->1+
$$\lim_{x \to 1^+}\left(- x^{4} + x^{2}\right)$$
0
$$0$$
= 1.63602817918362e-31
/ 2 4\ lim \x - x / x->1-
$$\lim_{x \to 1^-}\left(- x^{4} + x^{2}\right)$$
0
$$0$$
= 4.37637022617069e-30
= 4.37637022617069e-30
Other limits x→0, -oo, +oo, 1
$$\lim_{x \to 1^-}\left(- x^{4} + x^{2}\right) = 0$$
More at x→1 from the left
$$\lim_{x \to 1^+}\left(- x^{4} + x^{2}\right) = 0$$
$$\lim_{x \to \infty}\left(- x^{4} + x^{2}\right) = -\infty$$
More at x→oo
$$\lim_{x \to 0^-}\left(- x^{4} + x^{2}\right) = 0$$
More at x→0 from the left
$$\lim_{x \to 0^+}\left(- x^{4} + x^{2}\right) = 0$$
More at x→0 from the right
$$\lim_{x \to -\infty}\left(- x^{4} + x^{2}\right) = -\infty$$
More at x→-oo
More at x→1 from the left
$$\lim_{x \to 1^+}\left(- x^{4} + x^{2}\right) = 0$$
$$\lim_{x \to \infty}\left(- x^{4} + x^{2}\right) = -\infty$$
More at x→oo
$$\lim_{x \to 0^-}\left(- x^{4} + x^{2}\right) = 0$$
More at x→0 from the left
$$\lim_{x \to 0^+}\left(- x^{4} + x^{2}\right) = 0$$
More at x→0 from the right
$$\lim_{x \to -\infty}\left(- x^{4} + x^{2}\right) = -\infty$$
More at x→-oo
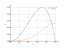
The graph