Mister Exam
Other calculators:
-
How to use it?
- Limit of the function:
-
Limit of (-5+7*n)/(2+n)
-
Limit of (-64+4^x)/(-3+x)
-
Limit of (-7+3*x^2+5*x)/(1+x+3*x^2)
-
Limit of (-2+2*x^3+7*x)/(-4-x+3*x^3)
- Derivative of:
-
x/sqrt(x^2+2*x)
-
Identical expressions
- x/sqrt(x^ two + two *x)
- x divide by square root of (x squared plus 2 multiply by x)
- x divide by square root of (x to the power of two plus two multiply by x)
- x/√(x^2+2*x)
- x/sqrt(x2+2*x)
- x/sqrtx2+2*x
- x/sqrt(x²+2*x)
- x/sqrt(x to the power of 2+2*x)
- x/sqrt(x^2+2x)
- x/sqrt(x2+2x)
- x/sqrtx2+2x
- x/sqrtx^2+2x
- x divide by sqrt(x^2+2*x)
-
Similar expressions
- x/sqrt(x^2-2*x)
Limit of the function x/sqrt(x^2+2*x)
The solution
You have entered
[src]
/ x \
lim |-------------|
x->oo| __________|
| / 2 |
\\/ x + 2*x /
$$\lim_{x \to \infty}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right)$$
Limit(x/sqrt(x^2 + 2*x), x, oo, dir='-')
Lopital's rule
We have indeterminateness of type
i.e. limit for the numerator is
$$\lim_{x \to \infty} x = \infty$$
and limit for the denominator is
$$\lim_{x \to \infty} \sqrt{x \left(x + 2\right)} = \infty$$
Let's take derivatives of the numerator and denominator until we eliminate indeterninateness.
$$\lim_{x \to \infty}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right)$$
=
Let's transform the function under the limit a few
$$\lim_{x \to \infty}\left(\frac{x}{\sqrt{x \left(x + 2\right)}}\right)$$
=
$$\lim_{x \to \infty}\left(\frac{\frac{d}{d x} x}{\frac{d}{d x} \sqrt{x \left(x + 2\right)}}\right)$$
=
$$\lim_{x \to \infty}\left(\frac{x \left(x + 2\right)}{\sqrt{x \left(x + 2\right)} \left(x + 1\right)}\right)$$
=
$$\lim_{x \to \infty}\left(\frac{\frac{d}{d x} \frac{x \left(x + 2\right)}{x + 1}}{\frac{d}{d x} \sqrt{x \left(x + 2\right)}}\right)$$
=
$$\lim_{x \to \infty}\left(\frac{- \frac{x^{2}}{x^{2} + 2 x + 1} - \frac{2 x}{x^{2} + 2 x + 1} + \frac{2 x}{x + 1} + \frac{2}{x + 1}}{\frac{x}{\sqrt{x^{2} + 2 x}} + \frac{1}{\sqrt{x^{2} + 2 x}}}\right)$$
=
$$\lim_{x \to \infty}\left(\frac{- \frac{x^{2}}{x^{2} + 2 x + 1} - \frac{2 x}{x^{2} + 2 x + 1} + \frac{2 x}{x + 1} + \frac{2}{x + 1}}{\frac{x}{\sqrt{x^{2} + 2 x}} + \frac{1}{\sqrt{x^{2} + 2 x}}}\right)$$
=
$$1$$
It can be seen that we have applied Lopital's rule (we have taken derivatives with respect to the numerator and denominator) 2 time(s)
oo/oo,
i.e. limit for the numerator is
$$\lim_{x \to \infty} x = \infty$$
and limit for the denominator is
$$\lim_{x \to \infty} \sqrt{x \left(x + 2\right)} = \infty$$
Let's take derivatives of the numerator and denominator until we eliminate indeterninateness.
$$\lim_{x \to \infty}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right)$$
=
Let's transform the function under the limit a few
$$\lim_{x \to \infty}\left(\frac{x}{\sqrt{x \left(x + 2\right)}}\right)$$
=
$$\lim_{x \to \infty}\left(\frac{\frac{d}{d x} x}{\frac{d}{d x} \sqrt{x \left(x + 2\right)}}\right)$$
=
$$\lim_{x \to \infty}\left(\frac{x \left(x + 2\right)}{\sqrt{x \left(x + 2\right)} \left(x + 1\right)}\right)$$
=
$$\lim_{x \to \infty}\left(\frac{\frac{d}{d x} \frac{x \left(x + 2\right)}{x + 1}}{\frac{d}{d x} \sqrt{x \left(x + 2\right)}}\right)$$
=
$$\lim_{x \to \infty}\left(\frac{- \frac{x^{2}}{x^{2} + 2 x + 1} - \frac{2 x}{x^{2} + 2 x + 1} + \frac{2 x}{x + 1} + \frac{2}{x + 1}}{\frac{x}{\sqrt{x^{2} + 2 x}} + \frac{1}{\sqrt{x^{2} + 2 x}}}\right)$$
=
$$\lim_{x \to \infty}\left(\frac{- \frac{x^{2}}{x^{2} + 2 x + 1} - \frac{2 x}{x^{2} + 2 x + 1} + \frac{2 x}{x + 1} + \frac{2}{x + 1}}{\frac{x}{\sqrt{x^{2} + 2 x}} + \frac{1}{\sqrt{x^{2} + 2 x}}}\right)$$
=
$$1$$
It can be seen that we have applied Lopital's rule (we have taken derivatives with respect to the numerator and denominator) 2 time(s)
The graph
Other limits x→0, -oo, +oo, 1
$$\lim_{x \to \infty}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right) = 1$$
$$\lim_{x \to 0^-}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right) = 0$$
More at x→0 from the left
$$\lim_{x \to 0^+}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right) = 0$$
More at x→0 from the right
$$\lim_{x \to 1^-}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right) = \frac{\sqrt{3}}{3}$$
More at x→1 from the left
$$\lim_{x \to 1^+}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right) = \frac{\sqrt{3}}{3}$$
More at x→1 from the right
$$\lim_{x \to -\infty}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right) = -1$$
More at x→-oo
$$\lim_{x \to 0^-}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right) = 0$$
More at x→0 from the left
$$\lim_{x \to 0^+}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right) = 0$$
More at x→0 from the right
$$\lim_{x \to 1^-}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right) = \frac{\sqrt{3}}{3}$$
More at x→1 from the left
$$\lim_{x \to 1^+}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right) = \frac{\sqrt{3}}{3}$$
More at x→1 from the right
$$\lim_{x \to -\infty}\left(\frac{x}{\sqrt{x^{2} + 2 x}}\right) = -1$$
More at x→-oo
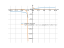
The graph