Mister Exam
Autres calculateurs:
-
Comment utiliser ?
- Limite d'une fonction:
-
Limite sin(5*x)
-
Limite ((1+2*x)/(-1+3*x))^(-1+x)
-
Limite -5-2*x+16*x^2/3
-
Limite cosh(n)/cosh(1+n)
- Graphe de la fonction y =:
- sin(5*x)
- Intégrale d{x}:
-
sin(5*x)
- Dérivée:
-
sin(5*x)
-
Expressions identiques
- sin(five *x)
- sinus de (5 multiplier par x)
- sinus de (five multiplier par x)
- sin(5x)
- sin5x
Limite d'une fonction sin(5*x)
Solution
You have entered
[src]
lim sin(5*x) x->0+
$$\lim_{x \to 0^+} \sin{\left(5 x \right)}$$
Limit(sin(5*x), x, 0)
Lopital's rule
There is no sense to apply Lopital's rule to this function since there is no indeterminateness of 0/0 or oo/oo type
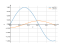
The graph
Other limits x→0, -oo, +oo, 1
$$\lim_{x \to 0^-} \sin{\left(5 x \right)} = 0$$
More at x→0 from the left
$$\lim_{x \to 0^+} \sin{\left(5 x \right)} = 0$$
$$\lim_{x \to \infty} \sin{\left(5 x \right)} = \left\langle -1, 1\right\rangle$$
More at x→oo
$$\lim_{x \to 1^-} \sin{\left(5 x \right)} = \sin{\left(5 \right)}$$
More at x→1 from the left
$$\lim_{x \to 1^+} \sin{\left(5 x \right)} = \sin{\left(5 \right)}$$
More at x→1 from the right
$$\lim_{x \to -\infty} \sin{\left(5 x \right)} = \left\langle -1, 1\right\rangle$$
More at x→-oo
More at x→0 from the left
$$\lim_{x \to 0^+} \sin{\left(5 x \right)} = 0$$
$$\lim_{x \to \infty} \sin{\left(5 x \right)} = \left\langle -1, 1\right\rangle$$
More at x→oo
$$\lim_{x \to 1^-} \sin{\left(5 x \right)} = \sin{\left(5 \right)}$$
More at x→1 from the left
$$\lim_{x \to 1^+} \sin{\left(5 x \right)} = \sin{\left(5 \right)}$$
More at x→1 from the right
$$\lim_{x \to -\infty} \sin{\left(5 x \right)} = \left\langle -1, 1\right\rangle$$
More at x→-oo
One‐sided limits
[src]
lim sin(5*x) x->0+
$$\lim_{x \to 0^+} \sin{\left(5 x \right)}$$
0
$$0$$
= -1.57784879884055e-29
lim sin(5*x) x->0-
$$\lim_{x \to 0^-} \sin{\left(5 x \right)}$$
0
$$0$$
= 1.57784879884055e-29
= 1.57784879884055e-29
Graphique