Mister Exam

Lang:

Other calculators

How to use it?
Integral of d{x}:
Integral of -e^x
Integral of -15x^2
Integral of xe^(1-x)
Integral of -xe^x
Identical expressions
(x+ two)^ two *cos(3x)
(x plus 2) squared multiply by co sinus of e of (3x)
(x plus two) to the power of two multiply by co sinus of e of (3x)
(x+2)2*cos(3x)
x+22*cos3x
(x+2)²*cos(3x)
(x+2) to the power of 2*cos(3x)
(x+2)^2cos(3x)
(x+2)2cos(3x)
x+22cos3x
x+2^2cos3x
(x+2)^2*cos(3x)dx
Similar expressions
(x-2)^2*cos(3x)

Solving integrals/ (x+2)^2*cos(3x)

Integral of (x+2)^2*cos(3x) dx

The solution

You have entered [src]

  0                     
  /                     
 |                      
 |         2            
 |  (x + 2) *cos(3*x) dx
 |                      
/                       
-2

$$\int\limits_{-2}^{0} \left(x + 2\right)^{2} \cos{\left(3 x \right)}\, dx$$

Integral((x + 2)^2*cos(3*x), (x, -2, 0))

Detail solution

There are multiple ways to do this integral.
Method #1
1. Rewrite the integrand:
  
  $\left(x + 2\right)^{2} \cos{\left(3 x \right)} = x^{2} \cos{\left(3 x \right)} + 4 x \cos{\left(3 x \right)} + 4 \cos{\left(3 x \right)}$
2. Integrate term-by-term:
  1. Use integration by parts:
    
    $\int \operatorname{u} \operatorname{dv} = \operatorname{u}\operatorname{v} - \int \operatorname{v} \operatorname{du}$
    
    Let $u{\left(x \right)} = x^{2}$ and let $\operatorname{dv}{\left(x \right)} = \cos{\left(3 x \right)}$ .
    
    Then $\operatorname{du}{\left(x \right)} = 2 x$ .
    
    To find $v{\left(x \right)}$ :
    1. Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\cos{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{3}\, du = \frac{\int \cos{\left(u \right)}\, du}{3}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(3 x \right)}}{3}$
    Now evaluate the sub-integral.
  2. Use integration by parts:
    
    $\int \operatorname{u} \operatorname{dv} = \operatorname{u}\operatorname{v} - \int \operatorname{v} \operatorname{du}$
    
    Let $u{\left(x \right)} = \frac{2 x}{3}$ and let $\operatorname{dv}{\left(x \right)} = \sin{\left(3 x \right)}$ .
    
    Then $\operatorname{du}{\left(x \right)} = \frac{2}{3}$ .
    
    To find $v{\left(x \right)}$ :
    1. Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\sin{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\sin{\left(u \right)}}{3}\, du = \frac{\int \sin{\left(u \right)}\, du}{3}$
      
      The integral of sine is negative cosine:
      
      $\int \sin{\left(u \right)}\, du = - \cos{\left(u \right)}$
      
      So, the result is: $- \frac{\cos{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $- \frac{\cos{\left(3 x \right)}}{3}$
    Now evaluate the sub-integral.
  3. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int \left(- \frac{2 \cos{\left(3 x \right)}}{9}\right)\, dx = - \frac{2 \int \cos{\left(3 x \right)}\, dx}{9}$
    1. Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\cos{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{3}\, du = \frac{\int \cos{\left(u \right)}\, du}{3}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(3 x \right)}}{3}$
    So, the result is: $- \frac{2 \sin{\left(3 x \right)}}{27}$
  1. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int 4 x \cos{\left(3 x \right)}\, dx = 4 \int x \cos{\left(3 x \right)}\, dx$
    1. Use integration by parts:
      
      $\int \operatorname{u} \operatorname{dv} = \operatorname{u}\operatorname{v} - \int \operatorname{v} \operatorname{du}$
      
      Let $u{\left(x \right)} = x$ and let $\operatorname{dv}{\left(x \right)} = \cos{\left(3 x \right)}$ .
      
      Then $\operatorname{du}{\left(x \right)} = 1$ .
      
      To find $v{\left(x \right)}$ :
      
      Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\cos{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{3}\, du = \frac{\int \cos{\left(u \right)}\, du}{3}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(3 x \right)}}{3}$
      
      Now evaluate the sub-integral.
    2. The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\sin{\left(3 x \right)}}{3}\, dx = \frac{\int \sin{\left(3 x \right)}\, dx}{3}$
      
      Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\sin{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\sin{\left(u \right)}}{3}\, du = \frac{\int \sin{\left(u \right)}\, du}{3}$
      
      The integral of sine is negative cosine:
      
      $\int \sin{\left(u \right)}\, du = - \cos{\left(u \right)}$
      
      So, the result is: $- \frac{\cos{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $- \frac{\cos{\left(3 x \right)}}{3}$
      
      So, the result is: $- \frac{\cos{\left(3 x \right)}}{9}$
    So, the result is: $\frac{4 x \sin{\left(3 x \right)}}{3} + \frac{4 \cos{\left(3 x \right)}}{9}$
  1. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int 4 \cos{\left(3 x \right)}\, dx = 4 \int \cos{\left(3 x \right)}\, dx$
    1. Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\cos{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{3}\, du = \frac{\int \cos{\left(u \right)}\, du}{3}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(3 x \right)}}{3}$
    So, the result is: $\frac{4 \sin{\left(3 x \right)}}{3}$
  The result is: $\frac{x^{2} \sin{\left(3 x \right)}}{3} + \frac{4 x \sin{\left(3 x \right)}}{3} + \frac{2 x \cos{\left(3 x \right)}}{9} + \frac{34 \sin{\left(3 x \right)}}{27} + \frac{4 \cos{\left(3 x \right)}}{9}$
Method #2
1. Use integration by parts:
  
  $\int \operatorname{u} \operatorname{dv} = \operatorname{u}\operatorname{v} - \int \operatorname{v} \operatorname{du}$
  
  Let $u{\left(x \right)} = x^{2} + 4 x + 4$ and let $\operatorname{dv}{\left(x \right)} = \cos{\left(3 x \right)}$ .
  
  Then $\operatorname{du}{\left(x \right)} = 2 x + 4$ .
  
  To find $v{\left(x \right)}$ :
  1. Let $u = 3 x$ .
    
    Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
    
    $\int \frac{\cos{\left(u \right)}}{9}\, du$
    1. The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{3}\, du = \frac{\int \cos{\left(u \right)}\, du}{3}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{3}$
    Now substitute $u$ back in:
    
    $\frac{\sin{\left(3 x \right)}}{3}$
  Now evaluate the sub-integral.
2. Use integration by parts:
  
  $\int \operatorname{u} \operatorname{dv} = \operatorname{u}\operatorname{v} - \int \operatorname{v} \operatorname{du}$
  
  Let $u{\left(x \right)} = \frac{2 x}{3} + \frac{4}{3}$ and let $\operatorname{dv}{\left(x \right)} = \sin{\left(3 x \right)}$ .
  
  Then $\operatorname{du}{\left(x \right)} = \frac{2}{3}$ .
  
  To find $v{\left(x \right)}$ :
  1. Let $u = 3 x$ .
    
    Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
    
    $\int \frac{\sin{\left(u \right)}}{9}\, du$
    1. The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\sin{\left(u \right)}}{3}\, du = \frac{\int \sin{\left(u \right)}\, du}{3}$
      
      The integral of sine is negative cosine:
      
      $\int \sin{\left(u \right)}\, du = - \cos{\left(u \right)}$
      
      So, the result is: $- \frac{\cos{\left(u \right)}}{3}$
    Now substitute $u$ back in:
    
    $- \frac{\cos{\left(3 x \right)}}{3}$
  Now evaluate the sub-integral.
3. The integral of a constant times a function is the constant times the integral of the function:
  
  $\int \left(- \frac{2 \cos{\left(3 x \right)}}{9}\right)\, dx = - \frac{2 \int \cos{\left(3 x \right)}\, dx}{9}$
  1. Let $u = 3 x$ .
    
    Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
    
    $\int \frac{\cos{\left(u \right)}}{9}\, du$
    1. The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{3}\, du = \frac{\int \cos{\left(u \right)}\, du}{3}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{3}$
    Now substitute $u$ back in:
    
    $\frac{\sin{\left(3 x \right)}}{3}$
  So, the result is: $- \frac{2 \sin{\left(3 x \right)}}{27}$
Method #3
1. Rewrite the integrand:
  
  $\left(x + 2\right)^{2} \cos{\left(3 x \right)} = x^{2} \cos{\left(3 x \right)} + 4 x \cos{\left(3 x \right)} + 4 \cos{\left(3 x \right)}$
2. Integrate term-by-term:
  1. Use integration by parts:
    
    $\int \operatorname{u} \operatorname{dv} = \operatorname{u}\operatorname{v} - \int \operatorname{v} \operatorname{du}$
    
    Let $u{\left(x \right)} = x^{2}$ and let $\operatorname{dv}{\left(x \right)} = \cos{\left(3 x \right)}$ .
    
    Then $\operatorname{du}{\left(x \right)} = 2 x$ .
    
    To find $v{\left(x \right)}$ :
    1. Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\cos{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{3}\, du = \frac{\int \cos{\left(u \right)}\, du}{3}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(3 x \right)}}{3}$
    Now evaluate the sub-integral.
  2. Use integration by parts:
    
    $\int \operatorname{u} \operatorname{dv} = \operatorname{u}\operatorname{v} - \int \operatorname{v} \operatorname{du}$
    
    Let $u{\left(x \right)} = \frac{2 x}{3}$ and let $\operatorname{dv}{\left(x \right)} = \sin{\left(3 x \right)}$ .
    
    Then $\operatorname{du}{\left(x \right)} = \frac{2}{3}$ .
    
    To find $v{\left(x \right)}$ :
    1. Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\sin{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\sin{\left(u \right)}}{3}\, du = \frac{\int \sin{\left(u \right)}\, du}{3}$
      
      The integral of sine is negative cosine:
      
      $\int \sin{\left(u \right)}\, du = - \cos{\left(u \right)}$
      
      So, the result is: $- \frac{\cos{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $- \frac{\cos{\left(3 x \right)}}{3}$
    Now evaluate the sub-integral.
  3. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int \left(- \frac{2 \cos{\left(3 x \right)}}{9}\right)\, dx = - \frac{2 \int \cos{\left(3 x \right)}\, dx}{9}$
    1. Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\cos{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{3}\, du = \frac{\int \cos{\left(u \right)}\, du}{3}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(3 x \right)}}{3}$
    So, the result is: $- \frac{2 \sin{\left(3 x \right)}}{27}$
  1. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int 4 x \cos{\left(3 x \right)}\, dx = 4 \int x \cos{\left(3 x \right)}\, dx$
    1. Use integration by parts:
      
      $\int \operatorname{u} \operatorname{dv} = \operatorname{u}\operatorname{v} - \int \operatorname{v} \operatorname{du}$
      
      Let $u{\left(x \right)} = x$ and let $\operatorname{dv}{\left(x \right)} = \cos{\left(3 x \right)}$ .
      
      Then $\operatorname{du}{\left(x \right)} = 1$ .
      
      To find $v{\left(x \right)}$ :
      
      Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\cos{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{3}\, du = \frac{\int \cos{\left(u \right)}\, du}{3}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(3 x \right)}}{3}$
      
      Now evaluate the sub-integral.
    2. The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\sin{\left(3 x \right)}}{3}\, dx = \frac{\int \sin{\left(3 x \right)}\, dx}{3}$
      
      Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\sin{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\sin{\left(u \right)}}{3}\, du = \frac{\int \sin{\left(u \right)}\, du}{3}$
      
      The integral of sine is negative cosine:
      
      $\int \sin{\left(u \right)}\, du = - \cos{\left(u \right)}$
      
      So, the result is: $- \frac{\cos{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $- \frac{\cos{\left(3 x \right)}}{3}$
      
      So, the result is: $- \frac{\cos{\left(3 x \right)}}{9}$
    So, the result is: $\frac{4 x \sin{\left(3 x \right)}}{3} + \frac{4 \cos{\left(3 x \right)}}{9}$
  1. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int 4 \cos{\left(3 x \right)}\, dx = 4 \int \cos{\left(3 x \right)}\, dx$
    1. Let $u = 3 x$ .
      
      Then let $du = 3 dx$ and substitute $\frac{du}{3}$ :
      
      $\int \frac{\cos{\left(u \right)}}{9}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{3}\, du = \frac{\int \cos{\left(u \right)}\, du}{3}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{3}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(3 x \right)}}{3}$
    So, the result is: $\frac{4 \sin{\left(3 x \right)}}{3}$
  The result is: $\frac{x^{2} \sin{\left(3 x \right)}}{3} + \frac{4 x \sin{\left(3 x \right)}}{3} + \frac{2 x \cos{\left(3 x \right)}}{9} + \frac{34 \sin{\left(3 x \right)}}{27} + \frac{4 \cos{\left(3 x \right)}}{9}$
Add the constant of integration:

$\frac{x^{2} \sin{\left(3 x \right)}}{3} + \frac{4 x \sin{\left(3 x \right)}}{3} + \frac{2 x \cos{\left(3 x \right)}}{9} + \frac{34 \sin{\left(3 x \right)}}{27} + \frac{4 \cos{\left(3 x \right)}}{9}+ \mathrm{constant}$

The answer is:

$\frac{x^{2} \sin{\left(3 x \right)}}{3} + \frac{4 x \sin{\left(3 x \right)}}{3} + \frac{2 x \cos{\left(3 x \right)}}{9} + \frac{34 \sin{\left(3 x \right)}}{27} + \frac{4 \cos{\left(3 x \right)}}{9}+ \mathrm{constant}$

The answer (Indefinite) [src]

  /                                                                                               
 |                                                        2                                       
 |        2                   4*cos(3*x)   34*sin(3*x)   x *sin(3*x)   2*x*cos(3*x)   4*x*sin(3*x)
 | (x + 2) *cos(3*x) dx = C + ---------- + ----------- + ----------- + ------------ + ------------
 |                                9             27            3             9              3      
/

$${{{{\left(9\,x^2-2\right)\,\sin \left(3\,x\right)+6\,x\,\cos \left( 3\,x\right)}\over{9}}+{{4\,\left(3\,x\,\sin \left(3\,x\right)+\cos \left(3\,x\right)\right)}\over{3}}+4\,\sin \left(3\,x\right)}\over{3 }}$$

Simplify

The graph

Plot the graph f(x)

The answer [src]

4   2*sin(6)
- - --------
9      27

$${{4}\over{9}}-{{2\,\sin 6}\over{27}}$$

4   2*sin(6)
- - --------
9      27

$$- \frac{2 \sin{\left(6 \right)}}{27} + \frac{4}{9}$$

Упростить

Numerical answer [src]

0.465141888755476

0.465141888755476

The graph

Use the examples entering the upper and lower limits of integration.

Other calculators

How to use it?

Identical expressions

Similar expressions

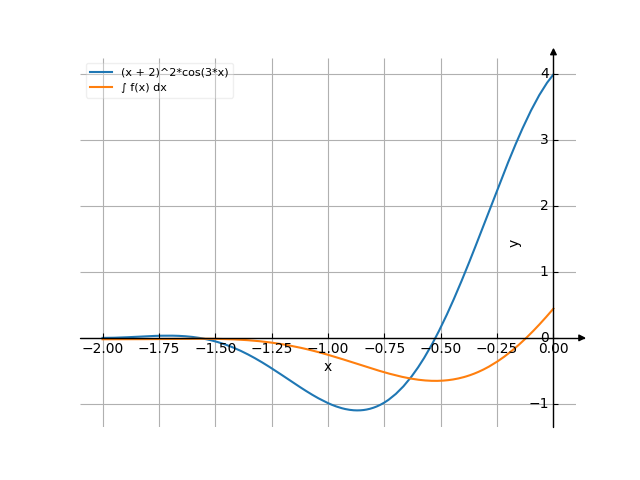
Integral of (x+2)^2*cos(3x) dx

Limits of integration:

The graph:

Piecewise:

The solution

Method #1

Method #2

Method #3