Mister Exam
Other calculators
- Improper integral
- Double Integral
- Triple Integral
- Curvilinear integral
- Derivative Step by Step
- Differential equations Step by Step
- Limits Step by Step
-
How to use it?
- Integral of d{x}:
-
Integral of 2
-
Integral of 5
-
Integral of e^(2x)
- Integral of x^n
-
Identical expressions
- sqrt(two -2e^(2x))
- square root of (2 minus 2e to the power of (2x))
- square root of (two minus 2e to the power of (2x))
- √(2-2e^(2x))
- sqrt(2-2e(2x))
- sqrt2-2e2x
- sqrt2-2e^2x
- sqrt(2-2e^(2x))dx
-
Similar expressions
- sqrt(2+2e^(2x))
Integral of sqrt(2-2e^(2x)) dx
The solution
You have entered
[src]
0
/
|
| ____________
| / 2*x
| \/ 2 - 2*e dx
|
/
-log(2)
--------
2
$$\int\limits_{- \frac{\log{\left(2 \right)}}{2}}^{0} \sqrt{2 - 2 e^{2 x}}\, dx$$
Integral(sqrt(2 - 2*E^(2*x)), (x, -log(2)/2, 0))
The answer (Indefinite)
[src]
/ | / / __________\ / __________\\ | ____________ | __________ | / 2*x | | / 2*x || | / 2*x ___ | / 2*x log\-1 + \/ 1 - e / log\1 + \/ 1 - e /| | \/ 2 - 2*e dx = C + \/ 2 *|\/ 1 - e + ----------------------- - ----------------------| | \ 2 2 / /
$$\int \sqrt{2 - 2 e^{2 x}}\, dx = C + \sqrt{2} \left(\sqrt{1 - e^{2 x}} + \frac{\log{\left(\sqrt{1 - e^{2 x}} - 1 \right)}}{2} - \frac{\log{\left(\sqrt{1 - e^{2 x}} + 1 \right)}}{2}\right)$$
The graph
The answer
[src]
/ / ___\ / ___\\
___ | ___ | \/ 2 | | \/ 2 ||
\/ 2 *|\/ 2 - log|1 + -----| + pi*I + log|1 - -----|| ___
\ \ 2 / \ 2 // pi*I*\/ 2
- ------------------------------------------------------ + ----------
2 2
$$- \frac{\sqrt{2} \left(\log{\left(1 - \frac{\sqrt{2}}{2} \right)} - \log{\left(\frac{\sqrt{2}}{2} + 1 \right)} + \sqrt{2} + i \pi\right)}{2} + \frac{\sqrt{2} i \pi}{2}$$
=
=
/ / ___\ / ___\\
___ | ___ | \/ 2 | | \/ 2 ||
\/ 2 *|\/ 2 - log|1 + -----| + pi*I + log|1 - -----|| ___
\ \ 2 / \ 2 // pi*I*\/ 2
- ------------------------------------------------------ + ----------
2 2
$$- \frac{\sqrt{2} \left(\log{\left(1 - \frac{\sqrt{2}}{2} \right)} - \log{\left(\frac{\sqrt{2}}{2} + 1 \right)} + \sqrt{2} + i \pi\right)}{2} + \frac{\sqrt{2} i \pi}{2}$$
The graph
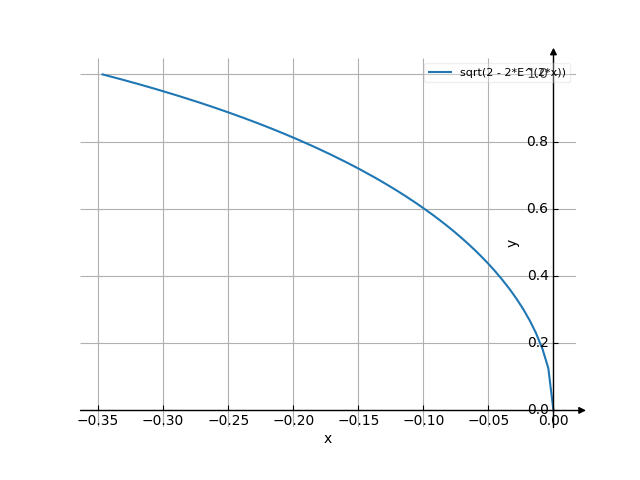
Use the examples entering the upper and lower limits of integration.