Integral of pi(sqrt(x)e^x)^2 dx
The solution
You have entered
[src]
1 / | | 2 | / ___ x\ | pi*\\/ x *e / dx | / 0
$$\int\limits_{0}^{1} \pi \left(\sqrt{x} e^{x}\right)^{2}\, dx$$
Integral(pi*(sqrt(x)*E^x)^2, (x, 0, 1))
Detail solution
-
The integral of a constant times a function is the constant times the integral of the function:
-
Don't know the steps in finding this integral.
But the integral is
So, the result is:
-
-
Add the constant of integration:
The answer is:
The answer (Indefinite)
[src]
/ | | 2 2*x | / ___ x\ pi*(-1 + 2*x)*e | pi*\\/ x *e / dx = C + ------------------ | 4 /
$${{\pi\,\left(2\,x-1\right)\,e^{2\,x}}\over{4}}$$
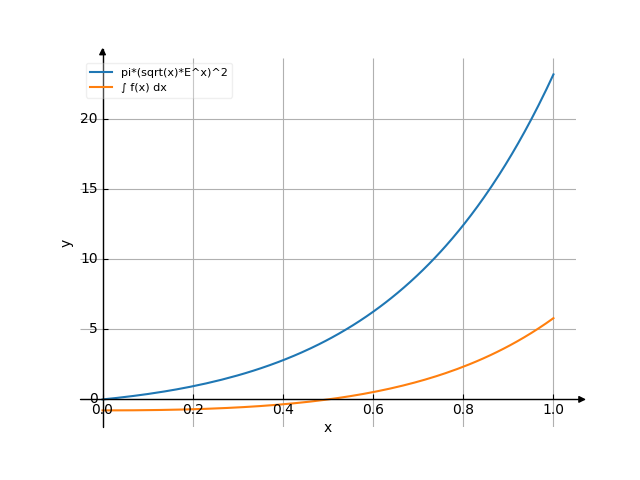
The graph
The answer
[src]
2 pi pi*e -- + ----- 4 4
$$\left({{e^2}\over{4}}+{{1}\over{4}}\right)\,\pi$$
=
=
2 pi pi*e -- + ----- 4 4
$$\frac{\pi}{4} + \frac{\pi e^{2}}{4}$$
The graph
Use the examples entering the upper and lower limits of integration.

![Find the integral of y = f(x) = pi(sqrt(x)e^x)² dx (Pi (square root of (x)e to the power of x) squared) - with detailed solution [THERE'S THE ANSWER!] pi(sqrt(x)e^x)^2](/media/krcore-image-pods/176/hash/indefinite/9/80/1bd416fd4220d92cdc6d41e7fcbda.png)
 Integral of (-1)/x^2
Integral of (-1)/x^2
 Integral of dy/y^2
Integral of dy/y^2
 Integral of (1+x^2)^1/2
Integral of (1+x^2)^1/2