Integral of cbrt(x) dx

You have entered [src]

  4         
  /         
 |          
 |  3 ___   
 |  \/ x  dx
 |          
/           
1

\int\limits_{1}^{4} \sqrt[3]{x}\, dx

Integral(x^(1/3), (x, 1, 4))

Detail solution

The integral of $x^{n}$ is $\frac{x^{n + 1}}{n + 1}$ when $n \neq -1$ :

$\int \sqrt[3]{x}\, dx = \frac{3 x^{\frac{4}{3}}}{4}$
Add the constant of integration:

$\frac{3 x^{\frac{4}{3}}}{4}+ \mathrm{constant}$

The answer is:

\frac{3 x^{\frac{4}{3}}}{4}+ \mathrm{constant}

The answer (Indefinite) [src]

  /                     
 |                   4/3
 | 3 ___          3*x   
 | \/ x  dx = C + ------
 |                  4   
/

{{3\,x^{{{4}\over{3}}}}\over{4}}

Simplify

The graph

Plot the graph f(x)

The answer [src]

  3      2/3
- - + 3*2   
  4

3\,4^{{{1}\over{3}}}-{{3}\over{4}}

  3      2/3
- - + 3*2   
  4

- \frac{3}{4} + 3 \cdot 2^{\frac{2}{3}}

Simplify

Numerical answer [src]

4.0122031559046

4.0122031559046

The graph

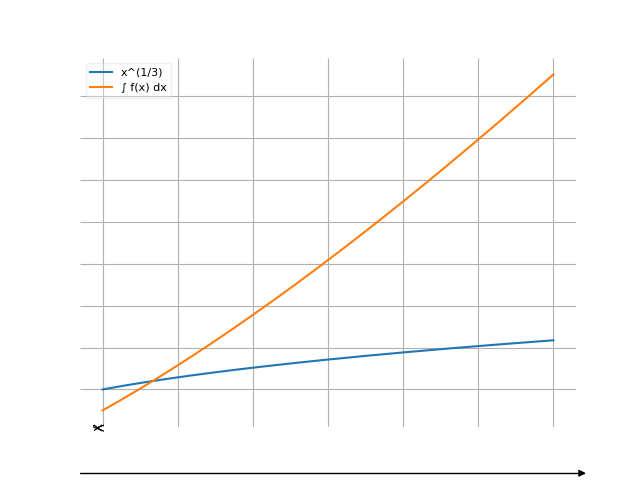
Use the examples entering the upper and lower limits of integration.