x^2*log512(4-x)>=log2(x^2-8x+16) inequation
The solution
You have entered
[src]
2 / 2 \ x *log(4 - x) log\x - 8*x + 16/ ------------- >= ------------------ log(512) log(2)
$$\frac{x^{2} \log{\left(- x + 4 \right)}}{\log{\left(512 \right)}} \geq \frac{\log{\left(x^{2} - 8 x + 16 \right)}}{\log{\left(2 \right)}}$$
x^2*log(4 - x)/log(512) >= log(x^2 - 8*x + 16)/log(2)
Detail solution
Given the inequality:
$$\frac{x^{2} \log{\left(- x + 4 \right)}}{\log{\left(512 \right)}} \geq \frac{\log{\left(x^{2} - 8 x + 16 \right)}}{\log{\left(2 \right)}}$$
To solve this inequality, we must first solve the corresponding equation:
$$\frac{x^{2} \log{\left(- x + 4 \right)}}{\log{\left(512 \right)}} = \frac{\log{\left(x^{2} - 8 x + 16 \right)}}{\log{\left(2 \right)}}$$
Solve:
$$x_{1} = 3$$
$$x_{2} = -4.24264068711928$$
$$x_{1} = 3$$
$$x_{2} = -4.24264068711928$$
This roots
$$x_{2} = -4.24264068711928$$
$$x_{1} = 3$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} \leq x_{2}$$
For example, let's take the point
$$x_{0} = x_{2} - \frac{1}{10}$$
=
$$-4.24264068711928 - \frac{1}{10}$$
=
$$-4.34264068711928$$
substitute to the expression
$$\frac{x^{2} \log{\left(- x + 4 \right)}}{\log{\left(512 \right)}} \geq \frac{\log{\left(x^{2} - 8 x + 16 \right)}}{\log{\left(2 \right)}}$$
$$\frac{\left(-4.34264068711928\right)^{2} \log{\left(4 - -4.34264068711928 \right)}}{\log{\left(512 \right)}} \geq \frac{\log{\left(16 + \left(-4.34264068711928\right)^{2} - 8 \left(-4.34264068711928\right) \right)}}{\log{\left(2 \right)}}$$
one of the solutions of our inequality is:
$$x \leq -4.24264068711928$$
Other solutions will get with the changeover to the next point
etc.
The answer:
$$x \leq -4.24264068711928$$
$$x \geq 3$$
$$\frac{x^{2} \log{\left(- x + 4 \right)}}{\log{\left(512 \right)}} \geq \frac{\log{\left(x^{2} - 8 x + 16 \right)}}{\log{\left(2 \right)}}$$
To solve this inequality, we must first solve the corresponding equation:
$$\frac{x^{2} \log{\left(- x + 4 \right)}}{\log{\left(512 \right)}} = \frac{\log{\left(x^{2} - 8 x + 16 \right)}}{\log{\left(2 \right)}}$$
Solve:
$$x_{1} = 3$$
$$x_{2} = -4.24264068711928$$
$$x_{1} = 3$$
$$x_{2} = -4.24264068711928$$
This roots
$$x_{2} = -4.24264068711928$$
$$x_{1} = 3$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} \leq x_{2}$$
For example, let's take the point
$$x_{0} = x_{2} - \frac{1}{10}$$
=
$$-4.24264068711928 - \frac{1}{10}$$
=
$$-4.34264068711928$$
substitute to the expression
$$\frac{x^{2} \log{\left(- x + 4 \right)}}{\log{\left(512 \right)}} \geq \frac{\log{\left(x^{2} - 8 x + 16 \right)}}{\log{\left(2 \right)}}$$
$$\frac{\left(-4.34264068711928\right)^{2} \log{\left(4 - -4.34264068711928 \right)}}{\log{\left(512 \right)}} \geq \frac{\log{\left(16 + \left(-4.34264068711928\right)^{2} - 8 \left(-4.34264068711928\right) \right)}}{\log{\left(2 \right)}}$$
40.0061005618117 4.24275959081044
---------------- >= ----------------
log(512) log(2) one of the solutions of our inequality is:
$$x \leq -4.24264068711928$$
_____ _____
\ /
-------•-------•-------
x_2 x_1Other solutions will get with the changeover to the next point
etc.
The answer:
$$x \leq -4.24264068711928$$
$$x \geq 3$$
Solving inequality on a graph

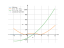 |x^2-3x-3|>x^2+7x-13
|x^2-3x-3|>x^2+7x-13
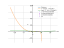 x^2log343(5-x)<log7(x^2-10x+25)
x^2log343(5-x)<log7(x^2-10x+25)
 8x²+24x>=0
8x²+24x>=0