|x^2-3x-3|>x^2+7x-13 inequation
The solution
You have entered
[src]
| 2 | 2 |x - 3*x - 3| > x + 7*x - 13
$$\left|{x^{2} - 3 x - 3}\right| > x^{2} + 7 x - 13$$
|x^2 - 3*x - 1*3| > x^2 + 7*x - 1*13
Detail solution
Given the inequality:
$$\left|{x^{2} - 3 x - 3}\right| > x^{2} + 7 x - 13$$
To solve this inequality, we must first solve the corresponding equation:
$$\left|{x^{2} - 3 x - 3}\right| = x^{2} + 7 x - 13$$
Solve:
For every modulo expressions in the equation
allow cases, when this expressions ">=0" or "<0",
solve the resulting equation.
1.
$$- x^{2} + 3 x + 3 \geq 0$$
or
$$x \leq \frac{3}{2} + \frac{\sqrt{21}}{2} \wedge \frac{3}{2} - \frac{\sqrt{21}}{2} \leq x$$
we get the equation
$$- x^{2} - 7 x + \left(- x^{2} + 3 x + 3\right) + 13 = 0$$
after simplifying we get
$$- 2 x^{2} - 4 x + 16 = 0$$
the solution in this interval:
$$x_{1} = -4$$
but x1 not in the inequality interval
$$x_{2} = 2$$
2.
$$- x^{2} + 3 x + 3 < 0$$
or
$$\left(-\infty < x \wedge x < \frac{3}{2} - \frac{\sqrt{21}}{2}\right) \vee \left(x < \infty \wedge \frac{3}{2} + \frac{\sqrt{21}}{2} < x\right)$$
we get the equation
$$- x^{2} - 7 x - \left(- x^{2} + 3 x + 3\right) + 13 = 0$$
after simplifying we get
$$- 10 x + 10 = 0$$
the solution in this interval:
$$x_{3} = 1$$
but x3 not in the inequality interval
$$x_{1} = 2$$
$$x_{1} = 2$$
This roots
$$x_{1} = 2$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$- \frac{1}{10} + 2$$
=
$$\frac{19}{10}$$
substitute to the expression
$$\left|{x^{2} - 3 x - 3}\right| > x^{2} + 7 x - 13$$
$$\left|{- \frac{3 \cdot 19}{10} - 3 + \left(\frac{19}{10}\right)^{2}}\right| > \left(-1\right) 13 + \left(\frac{19}{10}\right)^{2} + 7 \cdot \frac{19}{10}$$
the solution of our inequality is:
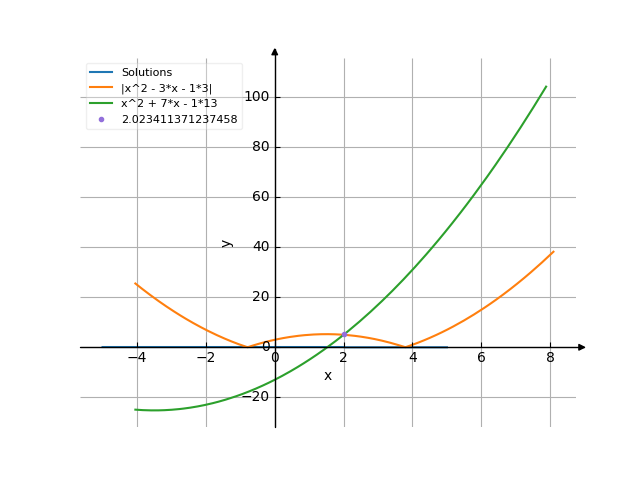
$$x < 2$$
$$\left|{x^{2} - 3 x - 3}\right| > x^{2} + 7 x - 13$$
To solve this inequality, we must first solve the corresponding equation:
$$\left|{x^{2} - 3 x - 3}\right| = x^{2} + 7 x - 13$$
Solve:
For every modulo expressions in the equation
allow cases, when this expressions ">=0" or "<0",
solve the resulting equation.
1.
$$- x^{2} + 3 x + 3 \geq 0$$
or
$$x \leq \frac{3}{2} + \frac{\sqrt{21}}{2} \wedge \frac{3}{2} - \frac{\sqrt{21}}{2} \leq x$$
we get the equation
$$- x^{2} - 7 x + \left(- x^{2} + 3 x + 3\right) + 13 = 0$$
after simplifying we get
$$- 2 x^{2} - 4 x + 16 = 0$$
the solution in this interval:
$$x_{1} = -4$$
but x1 not in the inequality interval
$$x_{2} = 2$$
2.
$$- x^{2} + 3 x + 3 < 0$$
or
$$\left(-\infty < x \wedge x < \frac{3}{2} - \frac{\sqrt{21}}{2}\right) \vee \left(x < \infty \wedge \frac{3}{2} + \frac{\sqrt{21}}{2} < x\right)$$
we get the equation
$$- x^{2} - 7 x - \left(- x^{2} + 3 x + 3\right) + 13 = 0$$
after simplifying we get
$$- 10 x + 10 = 0$$
the solution in this interval:
$$x_{3} = 1$$
but x3 not in the inequality interval
$$x_{1} = 2$$
$$x_{1} = 2$$
This roots
$$x_{1} = 2$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$- \frac{1}{10} + 2$$
=
$$\frac{19}{10}$$
substitute to the expression
$$\left|{x^{2} - 3 x - 3}\right| > x^{2} + 7 x - 13$$
$$\left|{- \frac{3 \cdot 19}{10} - 3 + \left(\frac{19}{10}\right)^{2}}\right| > \left(-1\right) 13 + \left(\frac{19}{10}\right)^{2} + 7 \cdot \frac{19}{10}$$
509 391 --- > --- 100 100
the solution of our inequality is:
$$x < 2$$
_____
\
-------ο-------
x_1
Solving inequality on a graph
The graph

![Solve the inequality |x²-3x-3|>x²+7x-13 (module of x squared minus 3x minus 3| greater than x squared plus 7x minus 13) - Specify the set of solutions of the inequality in detail step by step. [THERE'S THE ANSWER!] |x^2-3x-3|>x^2+7x-13](/media/krcore-image-pods/176/hash/inequation/d/57/44d3202b48aa25398ad1a5683ec85.png)
 (31-5*2^x)*1/(4^x-24*2^x+128)>=0,25
(31-5*2^x)*1/(4^x-24*2^x+128)>=0,25
 |x^2-3x-3|>x^2+7x-13
|x^2-3x-3|>x^2+7x-13
 x^2log343(5-x)<log7(x^2-10x+25)
x^2log343(5-x)<log7(x^2-10x+25)