tg^2x<9 inequation
The solution
Detail solution
Given the inequality:
$$\tan^{2}{\left(x \right)} < 9$$
To solve this inequality, we must first solve the corresponding equation:
$$\tan^{2}{\left(x \right)} = 9$$
Solve:
Given the equation
$$\tan^{2}{\left(x \right)} = 9$$
transform
$$\tan^{2}{\left(x \right)} - 9 = 0$$
$$\tan^{2}{\left(x \right)} - 9 = 0$$
Do replacement
$$w = \tan{\left(x \right)}$$
This equation is of the form
A quadratic equation can be solved
using the discriminant.
The roots of the quadratic equation:
$$w_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where D = b^2 - 4*a*c - it is the discriminant.
Because
$$a = 1$$
$$b = 0$$
$$c = -9$$
, then
Because D > 0, then the equation has two roots.
or
$$w_{1} = 3$$
$$w_{2} = -3$$
do backward replacement
$$\tan{\left(x \right)} = w$$
Given the equation
$$\tan{\left(x \right)} = w$$
- this is the simplest trigonometric equation
This equation is transformed to
$$x = \pi n + \operatorname{atan}{\left(w \right)}$$
Or
$$x = \pi n + \operatorname{atan}{\left(w \right)}$$
, where n - is a integer
substitute w:
$$x_{1} = \pi n + \operatorname{atan}{\left(w_{1} \right)}$$
$$x_{1} = \pi n + \operatorname{atan}{\left(3 \right)}$$
$$x_{1} = \pi n + \operatorname{atan}{\left(3 \right)}$$
$$x_{2} = \pi n + \operatorname{atan}{\left(w_{2} \right)}$$
$$x_{2} = \pi n + \operatorname{atan}{\left(-3 \right)}$$
$$x_{2} = \pi n - \operatorname{atan}{\left(3 \right)}$$
$$x_{1} = - \operatorname{atan}{\left(3 \right)}$$
$$x_{2} = \operatorname{atan}{\left(3 \right)}$$
$$x_{1} = - \operatorname{atan}{\left(3 \right)}$$
$$x_{2} = \operatorname{atan}{\left(3 \right)}$$
This roots
$$x_{1} = - \operatorname{atan}{\left(3 \right)}$$
$$x_{2} = \operatorname{atan}{\left(3 \right)}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(3 \right)} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(3 \right)} - \frac{1}{10}$$
substitute to the expression
$$\tan^{2}{\left(x \right)} < 9$$
$$\tan^{2}{\left(- \operatorname{atan}{\left(3 \right)} - \frac{1}{10} \right)} < 9$$
but
Then
$$x < - \operatorname{atan}{\left(3 \right)}$$
no execute
one of the solutions of our inequality is:
$$x > - \operatorname{atan}{\left(3 \right)} \wedge x < \operatorname{atan}{\left(3 \right)}$$
$$\tan^{2}{\left(x \right)} < 9$$
To solve this inequality, we must first solve the corresponding equation:
$$\tan^{2}{\left(x \right)} = 9$$
Solve:
Given the equation
$$\tan^{2}{\left(x \right)} = 9$$
transform
$$\tan^{2}{\left(x \right)} - 9 = 0$$
$$\tan^{2}{\left(x \right)} - 9 = 0$$
Do replacement
$$w = \tan{\left(x \right)}$$
This equation is of the form
a*w^2 + b*w + c = 0
A quadratic equation can be solved
using the discriminant.
The roots of the quadratic equation:
$$w_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where D = b^2 - 4*a*c - it is the discriminant.
Because
$$a = 1$$
$$b = 0$$
$$c = -9$$
, then
D = b^2 - 4 * a * c =
(0)^2 - 4 * (1) * (-9) = 36
Because D > 0, then the equation has two roots.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b - sqrt(D)) / (2*a)
or
$$w_{1} = 3$$
$$w_{2} = -3$$
do backward replacement
$$\tan{\left(x \right)} = w$$
Given the equation
$$\tan{\left(x \right)} = w$$
- this is the simplest trigonometric equation
This equation is transformed to
$$x = \pi n + \operatorname{atan}{\left(w \right)}$$
Or
$$x = \pi n + \operatorname{atan}{\left(w \right)}$$
, where n - is a integer
substitute w:
$$x_{1} = \pi n + \operatorname{atan}{\left(w_{1} \right)}$$
$$x_{1} = \pi n + \operatorname{atan}{\left(3 \right)}$$
$$x_{1} = \pi n + \operatorname{atan}{\left(3 \right)}$$
$$x_{2} = \pi n + \operatorname{atan}{\left(w_{2} \right)}$$
$$x_{2} = \pi n + \operatorname{atan}{\left(-3 \right)}$$
$$x_{2} = \pi n - \operatorname{atan}{\left(3 \right)}$$
$$x_{1} = - \operatorname{atan}{\left(3 \right)}$$
$$x_{2} = \operatorname{atan}{\left(3 \right)}$$
$$x_{1} = - \operatorname{atan}{\left(3 \right)}$$
$$x_{2} = \operatorname{atan}{\left(3 \right)}$$
This roots
$$x_{1} = - \operatorname{atan}{\left(3 \right)}$$
$$x_{2} = \operatorname{atan}{\left(3 \right)}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(3 \right)} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(3 \right)} - \frac{1}{10}$$
substitute to the expression
$$\tan^{2}{\left(x \right)} < 9$$
$$\tan^{2}{\left(- \operatorname{atan}{\left(3 \right)} - \frac{1}{10} \right)} < 9$$
2
tan (1/10 + atan(3)) < 9
but
2
tan (1/10 + atan(3)) > 9
Then
$$x < - \operatorname{atan}{\left(3 \right)}$$
no execute
one of the solutions of our inequality is:
$$x > - \operatorname{atan}{\left(3 \right)} \wedge x < \operatorname{atan}{\left(3 \right)}$$
_____
/ \
-------ο-------ο-------
x1 x2
Solving inequality on a graph
Rapid solution
[src]
Or(And(0 <= x, x < atan(3)), And(x <= pi, pi - atan(3) < x))
$$\left(0 \leq x \wedge x < \operatorname{atan}{\left(3 \right)}\right) \vee \left(x \leq \pi \wedge \pi - \operatorname{atan}{\left(3 \right)} < x\right)$$
((0 <= x)∧(x < atan(3)))∨((x <= pi)∧(pi - atan(3) < x))
Rapid solution 2
[src]
[0, atan(3)) U (pi - atan(3), pi]
$$x\ in\ \left[0, \operatorname{atan}{\left(3 \right)}\right) \cup \left(\pi - \operatorname{atan}{\left(3 \right)}, \pi\right]$$
x in Union(Interval.Ropen(0, atan(3)), Interval.Lopen(pi - atan(3), pi))

 tg^2x
tg^2x
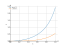 tg^2x
tg^2x