ctgx>700 inequation

You have entered [src]

cot(x) > 700

\cot{\left(x \right)} > 700

cot(x) > 700

Detail solution

Given the inequality:

\cot{\left(x \right)} > 700

To solve this inequality, we must first solve the corresponding equation:

\cot{\left(x \right)} = 700

Solve:
Given the equation

\cot{\left(x \right)} = 700

- this is the simplest trigonometric equation
This equation is transformed to

x = \pi n + \operatorname{acot}{\left(700 \right)}

Or

x = \pi n + \operatorname{acot}{\left(700 \right)}

, where n - is a integer

x_{1} = \pi n + \operatorname{acot}{\left(700 \right)}

x_{1} = \pi n + \operatorname{acot}{\left(700 \right)}

This roots

x_{1} = \pi n + \operatorname{acot}{\left(700 \right)}

is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:

x_{0} < x_{1}

For example, let's take the point

x_{0} = x_{1} - \frac{1}{10}

=

\left(\pi n + \operatorname{acot}{\left(700 \right)}\right) - \frac{1}{10}

=

\pi n - \frac{1}{10} + \operatorname{acot}{\left(700 \right)}

substitute to the expression

\cot{\left(x \right)} > 700

\cot{\left(\pi n - \frac{1}{10} + \operatorname{acot}{\left(700 \right)} \right)} > 700

-cot(1/10 - acot(700)) > 700

Then

x < \pi n + \operatorname{acot}{\left(700 \right)}

no execute
the solution of our inequality is:

x > \pi n + \operatorname{acot}{\left(700 \right)}

         _____  
        /
-------ο-------
       x_1

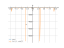
Solving inequality on a graph

Rapid solution [src]

And(0 < x, x < atan(1/700))

0 < x \wedge x < \operatorname{atan}{\left(\frac{1}{700} \right)}

(0 < x)∧(x < atan(1/700))

Rapid solution 2 [src]

(0, atan(1/700))

x\ in\ \left(0, \operatorname{atan}{\left(\frac{1}{700} \right)}\right)

x in Interval.open(0, atan(1/700))

The graph