cos(x)>(-2)/sqrt(3) inequation
The solution
You have entered
[src]
-2
cos(x) > -----
___
\/ 3
$$\cos{\left(x \right)} > - \frac{2}{\sqrt{3}}$$
cos(x) > -2*sqrt(3)/3
Detail solution
Given the inequality:
$$\cos{\left(x \right)} > - \frac{2}{\sqrt{3}}$$
To solve this inequality, we must first solve the corresponding equation:
$$\cos{\left(x \right)} = - \frac{2}{\sqrt{3}}$$
Solve:
Given the equation
$$\cos{\left(x \right)} = - \frac{2}{\sqrt{3}}$$
- this is the simplest trigonometric equation
As right part of the equation
modulo =
but cos
can no be more than 1 or less than -1
so the solution of the equation d'not exist.
$$x_{1} = 2 \pi - \operatorname{acos}{\left(- \frac{2 \sqrt{3}}{3} \right)}$$
$$x_{2} = \operatorname{acos}{\left(- \frac{2 \sqrt{3}}{3} \right)}$$
Exclude the complex solutions:
This equation has no roots,
this inequality is executed for any x value or has no solutions
check it
subtitute random point x, for example
$$\cos{\left(0 \right)} > - \frac{2}{\sqrt{3}}$$
so the inequality is always executed
$$\cos{\left(x \right)} > - \frac{2}{\sqrt{3}}$$
To solve this inequality, we must first solve the corresponding equation:
$$\cos{\left(x \right)} = - \frac{2}{\sqrt{3}}$$
Solve:
Given the equation
$$\cos{\left(x \right)} = - \frac{2}{\sqrt{3}}$$
- this is the simplest trigonometric equation
As right part of the equation
modulo =
True
but cos
can no be more than 1 or less than -1
so the solution of the equation d'not exist.
$$x_{1} = 2 \pi - \operatorname{acos}{\left(- \frac{2 \sqrt{3}}{3} \right)}$$
$$x_{2} = \operatorname{acos}{\left(- \frac{2 \sqrt{3}}{3} \right)}$$
Exclude the complex solutions:
This equation has no roots,
this inequality is executed for any x value or has no solutions
check it
subtitute random point x, for example
x0 = 0
$$\cos{\left(0 \right)} > - \frac{2}{\sqrt{3}}$$
___
-2*\/ 3
1 > --------
3
so the inequality is always executed
Solving inequality on a graph

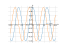 cos(x)
cos(x)
 cos(x)
cos(x)
 cos(x)
cos(x)