Graphing y = (x^2-1)/(x*3+1)
The solution
You have entered
[src]
2
x - 1
f(x) = -------
x*3 + 1
$$f{\left(x \right)} = \frac{x^{2} - 1}{3 x + 1}$$
f = (x^2 - 1)/(3*x + 1)
The graph of the function
The domain of the function
The points at which the function is not precisely defined:
$$x_{1} = -0.333333333333333$$
$$x_{1} = -0.333333333333333$$
The points of intersection with the X-axis coordinate
Graph of the function intersects the axis X at f = 0
so we need to solve the equation:
$$\frac{x^{2} - 1}{3 x + 1} = 0$$
Solve this equation
The points of intersection with the axis X:
Analytical solution
$$x_{1} = -1$$
$$x_{2} = 1$$
Numerical solution
$$x_{1} = 1$$
$$x_{2} = -1$$
so we need to solve the equation:
$$\frac{x^{2} - 1}{3 x + 1} = 0$$
Solve this equation
The points of intersection with the axis X:
Analytical solution
$$x_{1} = -1$$
$$x_{2} = 1$$
Numerical solution
$$x_{1} = 1$$
$$x_{2} = -1$$
Extrema of the function
In order to find the extrema, we need to solve the equation
$$\frac{d}{d x} f{\left(x \right)} = 0$$
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
$$\frac{d}{d x} f{\left(x \right)} = $$
the first derivative
$$\frac{2 x}{3 x + 1} - \frac{3 \left(x^{2} - 1\right)}{\left(3 x + 1\right)^{2}} = 0$$
Solve this equation
Solutions are not found,
function may have no extrema
$$\frac{d}{d x} f{\left(x \right)} = 0$$
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
$$\frac{d}{d x} f{\left(x \right)} = $$
the first derivative
$$\frac{2 x}{3 x + 1} - \frac{3 \left(x^{2} - 1\right)}{\left(3 x + 1\right)^{2}} = 0$$
Solve this equation
Solutions are not found,
function may have no extrema
Inflection points
Let's find the inflection points, we'll need to solve the equation for this
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = 0$$
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = $$
the second derivative
$$\frac{2 \left(- \frac{6 x}{3 x + 1} + 1 + \frac{9 \left(x^{2} - 1\right)}{\left(3 x + 1\right)^{2}}\right)}{3 x + 1} = 0$$
Solve this equation
Solutions are not found,
maybe, the function has no inflections
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = 0$$
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = $$
the second derivative
$$\frac{2 \left(- \frac{6 x}{3 x + 1} + 1 + \frac{9 \left(x^{2} - 1\right)}{\left(3 x + 1\right)^{2}}\right)}{3 x + 1} = 0$$
Solve this equation
Solutions are not found,
maybe, the function has no inflections
Vertical asymptotes
Have:
$$x_{1} = -0.333333333333333$$
$$x_{1} = -0.333333333333333$$
Horizontal asymptotes
Let’s find horizontal asymptotes with help of the limits of this function at x->+oo and x->-oo
$$\lim_{x \to -\infty}\left(\frac{x^{2} - 1}{3 x + 1}\right) = -\infty$$
Let's take the limit
so,
horizontal asymptote on the left doesn’t exist
$$\lim_{x \to \infty}\left(\frac{x^{2} - 1}{3 x + 1}\right) = \infty$$
Let's take the limit
so,
horizontal asymptote on the right doesn’t exist
$$\lim_{x \to -\infty}\left(\frac{x^{2} - 1}{3 x + 1}\right) = -\infty$$
Let's take the limit
so,
horizontal asymptote on the left doesn’t exist
$$\lim_{x \to \infty}\left(\frac{x^{2} - 1}{3 x + 1}\right) = \infty$$
Let's take the limit
so,
horizontal asymptote on the right doesn’t exist
Inclined asymptotes
Inclined asymptote can be found by calculating the limit of (x^2 - 1)/(x*3 + 1), divided by x at x->+oo and x ->-oo
$$\lim_{x \to -\infty}\left(\frac{x^{2} - 1}{x \left(3 x + 1\right)}\right) = \frac{1}{3}$$
Let's take the limit
so,
inclined asymptote equation on the left:
$$y = \frac{x}{3}$$
$$\lim_{x \to \infty}\left(\frac{x^{2} - 1}{x \left(3 x + 1\right)}\right) = \frac{1}{3}$$
Let's take the limit
so,
inclined asymptote equation on the right:
$$y = \frac{x}{3}$$
$$\lim_{x \to -\infty}\left(\frac{x^{2} - 1}{x \left(3 x + 1\right)}\right) = \frac{1}{3}$$
Let's take the limit
so,
inclined asymptote equation on the left:
$$y = \frac{x}{3}$$
$$\lim_{x \to \infty}\left(\frac{x^{2} - 1}{x \left(3 x + 1\right)}\right) = \frac{1}{3}$$
Let's take the limit
so,
inclined asymptote equation on the right:
$$y = \frac{x}{3}$$
Even and odd functions
Let's check, whether the function even or odd by using relations f = f(-x) и f = -f(-x).
So, check:
$$\frac{x^{2} - 1}{3 x + 1} = \frac{x^{2} - 1}{1 - 3 x}$$
- No
$$\frac{x^{2} - 1}{3 x + 1} = - \frac{x^{2} - 1}{1 - 3 x}$$
- No
so, the function
not is
neither even, nor odd
So, check:
$$\frac{x^{2} - 1}{3 x + 1} = \frac{x^{2} - 1}{1 - 3 x}$$
- No
$$\frac{x^{2} - 1}{3 x + 1} = - \frac{x^{2} - 1}{1 - 3 x}$$
- No
so, the function
not is
neither even, nor odd

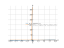 (x^2-1)/(x*3+1)
(x^2-1)/(x*3+1)