Graphing y = sqrt(3x)
The solution
The graph of the function
The points of intersection with the X-axis coordinate
Graph of the function intersects the axis X at f = 0
so we need to solve the equation:
$$\sqrt{3 x} = 0$$
Solve this equation
The points of intersection with the axis X:
Analytical solution
$$x_{1} = 0$$
Numerical solution
$$x_{1} = 0$$
so we need to solve the equation:
$$\sqrt{3 x} = 0$$
Solve this equation
The points of intersection with the axis X:
Analytical solution
$$x_{1} = 0$$
Numerical solution
$$x_{1} = 0$$
Extrema of the function
In order to find the extrema, we need to solve the equation
$$\frac{d}{d x} f{\left(x \right)} = 0$$
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
$$\frac{d}{d x} f{\left(x \right)} = $$
the first derivative
$$\frac{\sqrt{3} \sqrt{x}}{2 x} = 0$$
Solve this equation
Solutions are not found,
function may have no extrema
$$\frac{d}{d x} f{\left(x \right)} = 0$$
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
$$\frac{d}{d x} f{\left(x \right)} = $$
the first derivative
$$\frac{\sqrt{3} \sqrt{x}}{2 x} = 0$$
Solve this equation
Solutions are not found,
function may have no extrema
Inflection points
Let's find the inflection points, we'll need to solve the equation for this
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = 0$$
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = $$
the second derivative
$$- \frac{\sqrt{3}}{4 x^{\frac{3}{2}}} = 0$$
Solve this equation
Solutions are not found,
maybe, the function has no inflections
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = 0$$
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = $$
the second derivative
$$- \frac{\sqrt{3}}{4 x^{\frac{3}{2}}} = 0$$
Solve this equation
Solutions are not found,
maybe, the function has no inflections
Horizontal asymptotes
Let’s find horizontal asymptotes with help of the limits of this function at x->+oo and x->-oo
$$\lim_{x \to -\infty} \sqrt{3 x} = \infty i$$
Let's take the limit
so,
horizontal asymptote on the left doesn’t exist
$$\lim_{x \to \infty} \sqrt{3 x} = \infty$$
Let's take the limit
so,
horizontal asymptote on the right doesn’t exist
$$\lim_{x \to -\infty} \sqrt{3 x} = \infty i$$
Let's take the limit
so,
horizontal asymptote on the left doesn’t exist
$$\lim_{x \to \infty} \sqrt{3 x} = \infty$$
Let's take the limit
so,
horizontal asymptote on the right doesn’t exist
Inclined asymptotes
Inclined asymptote can be found by calculating the limit of sqrt(3*x), divided by x at x->+oo and x ->-oo
$$\lim_{x \to -\infty}\left(\frac{\sqrt{3} \sqrt{x}}{x}\right) = 0$$
Let's take the limit
so,
inclined coincides with the horizontal asymptote on the right
$$\lim_{x \to \infty}\left(\frac{\sqrt{3} \sqrt{x}}{x}\right) = 0$$
Let's take the limit
so,
inclined coincides with the horizontal asymptote on the left
$$\lim_{x \to -\infty}\left(\frac{\sqrt{3} \sqrt{x}}{x}\right) = 0$$
Let's take the limit
so,
inclined coincides with the horizontal asymptote on the right
$$\lim_{x \to \infty}\left(\frac{\sqrt{3} \sqrt{x}}{x}\right) = 0$$
Let's take the limit
so,
inclined coincides with the horizontal asymptote on the left
Even and odd functions
Let's check, whether the function even or odd by using relations f = f(-x) и f = -f(-x).
So, check:
$$\sqrt{3 x} = \sqrt{3} \sqrt{- x}$$
- No
$$\sqrt{3 x} = - \sqrt{3} \sqrt{- x}$$
- No
so, the function
not is
neither even, nor odd
So, check:
$$\sqrt{3 x} = \sqrt{3} \sqrt{- x}$$
- No
$$\sqrt{3 x} = - \sqrt{3} \sqrt{- x}$$
- No
so, the function
not is
neither even, nor odd

 4x^3-2x^2
4x^3-2x^2
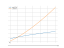 sqrt(3x)
sqrt(3x)
 sqrt(3x)
sqrt(3x)