√3tgx/3-1=0 equation
The teacher will be very surprised to see your correct solution 😉
The solution
Detail solution
Given the equation
transform
Do replacement
Given the equation
Because equation degree is equal to = 1/2 - does not contain even numbers in the numerator, then
the equation has single real root.
We raise the equation sides to 2-th degree:
We get:
or
Divide both parts of the equation by 1/3
We get the answer: w = 3
The final answer:
do backward replacement
Given the equation
- this is the simplest trigonometric equation
This equation is transformed to
Or
, where n - is a integer
substitute w:
transform
Do replacement
Given the equation
Because equation degree is equal to = 1/2 - does not contain even numbers in the numerator, then
the equation has single real root.
We raise the equation sides to 2-th degree:
We get:
or
Divide both parts of the equation by 1/3
w = 1 / (1/3)
We get the answer: w = 3
The final answer:
do backward replacement
Given the equation
- this is the simplest trigonometric equation
This equation is transformed to
Or
, where n - is a integer
substitute w:
Numerical answer
[src]
x1 = -8.17573218837112
x2 = -86.715548528116
x3 = -64.7243999529874
x4 = 32.6649723082962
x5 = -39.5916587242691
x6 = -17.6005101491405
x7 = 98.6384180336818
x8 = 79.7888621121431
x9 = 57.7977135370145
x10 = -55.299621992218
x11 = 20.098601693937
x12 = -45.8748440314486
x13 = 26.3817870011166
x14 = 48.3729355762452
x15 = -20.7421028027303
x16 = 86.0720474193227
x17 = -99.2819191424751
x18 = -42.7332513778588
x19 = 45.2313429226554
x20 = 4.39063842598805
x21 = -33.3084734170895
x22 = -1.89254688119154
x23 = 35.806564961886
x24 = 42.0897502690656
x25 = -67.8659926065772
x26 = -74.1491779137568
x27 = 13.8154163867574
x28 = -52.1580293386282
x29 = 92.3552327265023
x30 = -77.2907705673466
x31 = -89.8571411817058
x32 = 89.2136400729125
x33 = -61.5828072993976
x34 = 54.6561208834247
x35 = 64.0808988441941
x36 = 70.3640841513737
x37 = 23.2401943475268
x38 = -11.3173248419609
x39 = -96.1403264888853
x40 = -83.5739558745262
x41 = -92.9987338352955
x42 = 76.6472694585533
x43 = 67.2224914977839
x44 = -23.8836954563201
x45 = 10.6738237331676
x46 = 1.24904577239825
x47 = -30.1668807634997
x47 = -30.1668807634997

 Equation 1-5*x=-6*x+8
Equation 1-5*x=-6*x+8
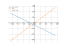 Equation -2x-4=3x
Equation -2x-4=3x
 Equation -3x-9=2x
Equation -3x-9=2x
 Equation 9x-26=30-5x
Equation 9x-26=30-5x