Mister Exam

Lang:

Other calculators

How to use it?
Equation:
Equation sqrt(((3)/20-5x))=0,2
Equation cos(pi/2-9x/2)cos(x/2)+sin(pi+x/2)cos(9x/2)=sin^2(4x)
Equation (2y)/(y-3)=(3y+3)/y
Equation ctg(x)
Express {x} in terms of y where:
9*x+18*y=6
15*x-15*y=16
sqrt(x^2+y^2+4x-6y-12)+(x^2+10x-27)=8-|y-9|+|y-3|
(x^2+y^2-1)^3+x^2*y^3=0
Sum of series:
0,2
Integral of d{x}:
0,2
Identical expressions
sqrt(((three)/ twenty -5x))= zero , two
square root of (((3) divide by 20 minus 5x)) equally 0,2
square root of (((three) divide by twenty minus 5x)) equally zero , two
√(((3)/20-5x))=0,2
sqrt3/20-5x=0,2
sqrt(((3)/20-5x))=O,2
sqrt(((3) divide by 20-5x))=0,2
Similar expressions
sqrt(((3)/20+5x))=0,2
What you mean?
sqrt(3/(20 - 5*x)) = 1/5
sqrt(3*x/(20 - 1*5)) = 1/5
sqrt(-5*x + 3/20) = 1/5
sqrt(-5*x + 3/20) = 1/5

You entered:

sqrt(((3)/20-5x))=0,2

What you mean?

sqrt(3/(20 - 5*x)) = 1/5

sqrt(3*x/(20 - 1*5)) = 1/5

sqrt(-5*x + 3/20) = 1/5

sqrt(-5*x + 3/20) = 1/5

sqrt(((3)/20-5x))=0,2 equation

The teacher will be very surprised to see your correct solution 😉

The solution

You have entered [src]

    __________      
   / 3              
  /  -- - 5*x  = 1/5
\/   20

\sqrt{- 5 x + \frac{3}{20}} = \frac{1}{5}

Simplify

Detail solution

Given the equation

\sqrt{- 5 x + \frac{3}{20}} = \frac{1}{5}

Because equation degree is equal to = 1/2 - does not contain even numbers in the numerator, then
the equation has single real root.
We raise the equation sides to 2-th degree:
We get:

\left(\sqrt{- 5 x + \frac{3}{20}}\right)^{2} = \left(\frac{1}{5}\right)^{2}

- 5 x + \frac{3}{20} = \frac{1}{25}

Move free summands (without x)
from left part to right part, we given:

- 5 x = - \frac{11}{100}

Divide both parts of the equation by -5

x = -11/100 / (-5)

We get the answer: x = 11/500

The final answer:

x_{1} = \frac{11}{500}

The graph

Plot the graph f1(x)

Plot the graph f2(x)

Rapid solution [src]

       11
x_1 = ---
      500

x_{1} = \frac{11}{500}

Simplify

Sum and product of roots [src]

sum

 11
---
500

\left(\frac{11}{500}\right)

 11
---
500

\frac{11}{500}

Simplify

product

 11
---
500

\left(\frac{11}{500}\right)

 11
---
500

\frac{11}{500}

Simplify

Numerical answer [src]

x1 = 0.022

x1 = 0.022

The graph

Other calculators

How to use it?

Identical expressions

Similar expressions

What you mean?

You entered:

What you mean?

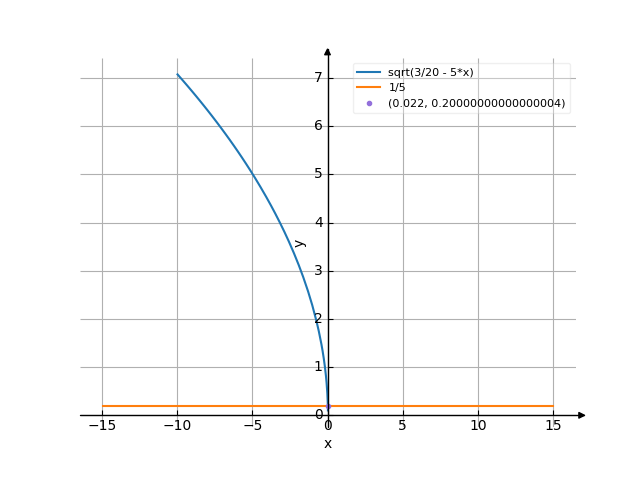
sqrt(((3)/20-5x))=0,2 equation

Numerical solution:

The solution