lnx+1-2x=0 equation
The teacher will be very surprised to see your correct solution 😉
The solution
Rapid solution
[src]
/ / -1\\ / / -1\\
re\W\-2*e // I*im\W\-2*e //
x_1 = - ------------- - ---------------
2 2
$$x_{1} = - \frac{\operatorname{re}{\left(W\left(- \frac{2}{e}\right)\right)}}{2} - \frac{i \operatorname{im}{\left(W\left(- \frac{2}{e}\right)\right)}}{2}$$
Sum and product of roots
[src]
sum
/ / -1\\ / / -1\\
re\W\-2*e // I*im\W\-2*e //
- ------------- - ---------------
2 2
$$\left(- \frac{\operatorname{re}{\left(W\left(- \frac{2}{e}\right)\right)}}{2} - \frac{i \operatorname{im}{\left(W\left(- \frac{2}{e}\right)\right)}}{2}\right)$$
=
/ / -1\\ / / -1\\
re\W\-2*e // I*im\W\-2*e //
- ------------- - ---------------
2 2
$$- \frac{\operatorname{re}{\left(W\left(- \frac{2}{e}\right)\right)}}{2} - \frac{i \operatorname{im}{\left(W\left(- \frac{2}{e}\right)\right)}}{2}$$
product
/ / -1\\ / / -1\\
re\W\-2*e // I*im\W\-2*e //
- ------------- - ---------------
2 2
$$\left(- \frac{\operatorname{re}{\left(W\left(- \frac{2}{e}\right)\right)}}{2} - \frac{i \operatorname{im}{\left(W\left(- \frac{2}{e}\right)\right)}}{2}\right)$$
=
/ / -1\\ / / -1\\
re\W\-2*e // I*im\W\-2*e //
- ------------- - ---------------
2 2
$$- \frac{\operatorname{re}{\left(W\left(- \frac{2}{e}\right)\right)}}{2} - \frac{i \operatorname{im}{\left(W\left(- \frac{2}{e}\right)\right)}}{2}$$
Numerical answer
[src]
x1 = 0.265323182170863 + 0.566336248802441*i
x1 = 0.265323182170863 + 0.566336248802441*i
The graph


![Solve the equation lnx+1-2x=0 (lnx plus 1 minus 2x equally 0) - Find the roots of the equation in detail step by step. [THERE'S THE ANSWER!] lnx+1-2x=0](/media/krcore-image-pods/176/hash/equation/2/36/fd63719b7af9e31eb1313d4e2eb0a.png)
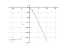 Equation lnx+1-2x=0
Equation lnx+1-2x=0