ln(x)=0.5x equation
The teacher will be very surprised to see your correct solution 😉
The solution
Rapid solution
[src]
x1 = -2*re(W(-1/2)) - 2*I*im(W(-1/2))
$$x_{1} = - 2 \operatorname{re}{\left(W\left(- \frac{1}{2}\right)\right)} - 2 i \operatorname{im}{\left(W\left(- \frac{1}{2}\right)\right)}$$
x1 = -2*re(LambertW(-1/2)) - 2*i*im(LambertW(-1/2))
Sum and product of roots
[src]
sum
-2*re(W(-1/2)) - 2*I*im(W(-1/2))
$$- 2 \operatorname{re}{\left(W\left(- \frac{1}{2}\right)\right)} - 2 i \operatorname{im}{\left(W\left(- \frac{1}{2}\right)\right)}$$
=
-2*re(W(-1/2)) - 2*I*im(W(-1/2))
$$- 2 \operatorname{re}{\left(W\left(- \frac{1}{2}\right)\right)} - 2 i \operatorname{im}{\left(W\left(- \frac{1}{2}\right)\right)}$$
product
-2*re(W(-1/2)) - 2*I*im(W(-1/2))
$$- 2 \operatorname{re}{\left(W\left(- \frac{1}{2}\right)\right)} - 2 i \operatorname{im}{\left(W\left(- \frac{1}{2}\right)\right)}$$
=
-2*re(W(-1/2)) - 2*I*im(W(-1/2))
$$- 2 \operatorname{re}{\left(W\left(- \frac{1}{2}\right)\right)} - 2 i \operatorname{im}{\left(W\left(- \frac{1}{2}\right)\right)}$$
-2*re(LambertW(-1/2)) - 2*i*im(LambertW(-1/2))
Numerical answer
[src]
x1 = 1.58804726468938 + 1.54022350102076*i
x1 = 1.58804726468938 + 1.54022350102076*i

 Equation x^2=-74
Equation x^2=-74
 Equation sin(6*x-pi/6)=1/2
Equation sin(6*x-pi/6)=1/2
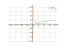 ln(x)
ln(x)
 0.5x
0.5x