Mister Exam
Other calculators
-
How to use it?
- Equation:
-
Equation -x/12+x=55/12
- Equation x-y=1
-
Equation 3(x+3)=2x+5
-
Equation 8-5(2x-3)=13-6x
- Express {x} in terms of y where:
- -4*x+6*y=-7
- -7*x-13*y=5
- 6*x+1*y=14
- 14*x-3*y=-5
-
Identical expressions
- (k- three)/ four =(three k-3)/ eleven
- (k minus 3) divide by 4 equally (3k minus 3) divide by 11
- (k minus three) divide by four equally (three k minus 3) divide by eleven
- k-3/4=3k-3/11
- (k-3) divide by 4=(3k-3) divide by 11
-
Similar expressions
- (k-3)/4=(3k+3)/11
- (k+3)/4=(3k-3)/11
(k-3)/4=(3k-3)/11 equation
The teacher will be very surprised to see your correct solution 😉
The solution
Detail solution
Given the linear equation:
Expand brackets in the left part
Expand brackets in the right part
Move free summands (without k)
from left part to right part, we given:
$$\frac{k}{4} = \frac{3 k}{11} + \frac{21}{44}$$
Move the summands with the unknown k
from the right part to the left part:
$$- \frac{k}{44} = \frac{21}{44}$$
Divide both parts of the equation by -1/44
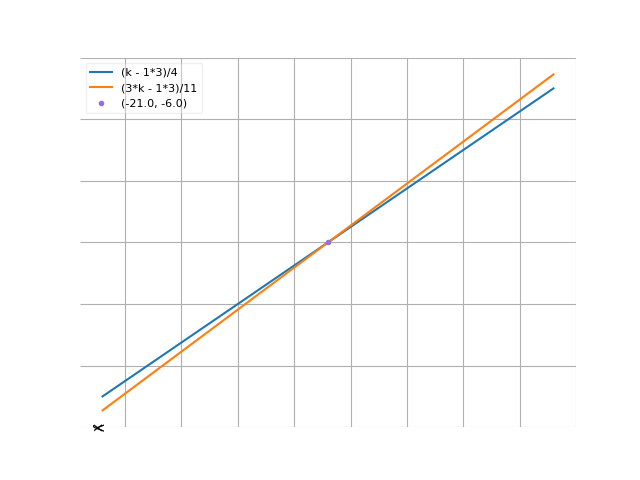
We get the answer: k = -21
(k-3)/4 = (3*k-3)/11
Expand brackets in the left part
k/4-3/4 = (3*k-3)/11
Expand brackets in the right part
k/4-3/4 = 3*k/11-3/11
Move free summands (without k)
from left part to right part, we given:
$$\frac{k}{4} = \frac{3 k}{11} + \frac{21}{44}$$
Move the summands with the unknown k
from the right part to the left part:
$$- \frac{k}{44} = \frac{21}{44}$$
Divide both parts of the equation by -1/44
k = 21/44 / (-1/44)
We get the answer: k = -21
Sum and product of roots
[src]
sum
-21
$$\left(-21\right)$$
=
-21
$$-21$$
product
-21
$$\left(-21\right)$$
=
-21
$$-21$$
The graph