Mister Exam
Other calculators
-
How to use it?
- Equation:
-
Equation (5x+2)(-x-4)=0
-
Equation sin(x)=3/4
-
Equation 9-2*(-4*x+7)=7
-
Equation x^2-4x+5=0
- Express {x} in terms of y where:
- -11*x+10*y=-9
- -9*x-4*y=-20
- 4*x-7*y=4
- -6*x-12*y=9
- Integral of d{x}:
-
cos(x)^(2)
- Derivative of:
-
cos(x)^(2)
-
3/4
- Graphing y =:
- cos(x)^(2)
- Sum of series:
-
3/4
- Limit of the function:
-
3/4
-
Identical expressions
- cos(x)^(two)= three / four
- co sinus of e of (x) to the power of (2) equally 3 divide by 4
- co sinus of e of (x) to the power of (two) equally three divide by four
- cos(x)(2)=3/4
- cosx2=3/4
- cosx^2=3/4
- cos(x)^(2)=3 divide by 4
-
Similar expressions
- 2sinx^3+2√2cosx^2+sinx=2√2
- cos(x^2)=0
- (k-3)/4=(3k-3)/11
- sin(x)*cos(x^2-18^0)^(2)*log(x)=0
- cosx^(2)=3/4
cos(x)^(2)=3/4 equation
The teacher will be very surprised to see your correct solution 😉
The solution
Detail solution
Given the equation
$$\cos^{2}{\left(x \right)} = \frac{3}{4}$$
transform
$$\cos^{2}{\left(x \right)} - \frac{3}{4} = 0$$
$$\cos^{2}{\left(x \right)} - \frac{3}{4} = 0$$
Do replacement
$$w = \cos{\left(x \right)}$$
This equation is of the form
$$a\ w^2 + b\ w + c = 0$$
A quadratic equation can be solved using the discriminant
The roots of the quadratic equation:
$$w_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where $D = b^2 - 4 a c$ is the discriminant.
Because
$$a = 1$$
$$b = 0$$
$$c = - \frac{3}{4}$$
, then
$$D = b^2 - 4\ a\ c = $$
$$0^{2} - 1 \cdot 4 \left(- \frac{3}{4}\right) = 3$$
Because D > 0, then the equation has two roots.
$$w_1 = \frac{(-b + \sqrt{D})}{2 a}$$
$$w_2 = \frac{(-b - \sqrt{D})}{2 a}$$
or
$$w_{1} = \frac{\sqrt{3}}{2}$$
Simplify
$$w_{2} = - \frac{\sqrt{3}}{2}$$
Simplify
do backward replacement
$$\cos{\left(x \right)} = w$$
$$\cos{\left(x \right)} = w$$
- this is the simplest trigonometric equation
This equation is transformed to
$$x = 2 \pi n + \operatorname{acos}{\left(w \right)}$$
$$x = 2 \pi n + \operatorname{acos}{\left(w \right)} - \pi$$
Or
$$x = 2 \pi n + \operatorname{acos}{\left(w \right)}$$
$$x = 2 \pi n + \operatorname{acos}{\left(w \right)} - \pi$$
, where n - is a integer
substitute w:
$$x_{1} = 2 \pi n + \operatorname{acos}{\left(w_{1} \right)}$$
$$x_{1} = 2 \pi n + \operatorname{acos}{\left(\frac{\sqrt{3}}{2} \right)}$$
$$x_{1} = 2 \pi n + \frac{\pi}{6}$$
$$x_{2} = 2 \pi n + \operatorname{acos}{\left(w_{2} \right)}$$
$$x_{2} = 2 \pi n + \operatorname{acos}{\left(- \frac{\sqrt{3}}{2} \right)}$$
$$x_{2} = 2 \pi n + \frac{5 \pi}{6}$$
$$x_{3} = 2 \pi n + \operatorname{acos}{\left(w_{1} \right)} - \pi$$
$$x_{3} = 2 \pi n - \pi + \operatorname{acos}{\left(\frac{\sqrt{3}}{2} \right)}$$
$$x_{3} = 2 \pi n - \frac{5 \pi}{6}$$
$$x_{4} = 2 \pi n + \operatorname{acos}{\left(w_{2} \right)} - \pi$$
$$x_{4} = 2 \pi n - \pi + \operatorname{acos}{\left(- \frac{\sqrt{3}}{2} \right)}$$
$$x_{4} = 2 \pi n - \frac{\pi}{6}$$
$$\cos^{2}{\left(x \right)} = \frac{3}{4}$$
transform
$$\cos^{2}{\left(x \right)} - \frac{3}{4} = 0$$
$$\cos^{2}{\left(x \right)} - \frac{3}{4} = 0$$
Do replacement
$$w = \cos{\left(x \right)}$$
This equation is of the form
$$a\ w^2 + b\ w + c = 0$$
A quadratic equation can be solved using the discriminant
The roots of the quadratic equation:
$$w_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where $D = b^2 - 4 a c$ is the discriminant.
Because
$$a = 1$$
$$b = 0$$
$$c = - \frac{3}{4}$$
, then
$$D = b^2 - 4\ a\ c = $$
$$0^{2} - 1 \cdot 4 \left(- \frac{3}{4}\right) = 3$$
Because D > 0, then the equation has two roots.
$$w_1 = \frac{(-b + \sqrt{D})}{2 a}$$
$$w_2 = \frac{(-b - \sqrt{D})}{2 a}$$
or
$$w_{1} = \frac{\sqrt{3}}{2}$$
Simplify
$$w_{2} = - \frac{\sqrt{3}}{2}$$
Simplify
do backward replacement
$$\cos{\left(x \right)} = w$$
$$\cos{\left(x \right)} = w$$
- this is the simplest trigonometric equation
This equation is transformed to
$$x = 2 \pi n + \operatorname{acos}{\left(w \right)}$$
$$x = 2 \pi n + \operatorname{acos}{\left(w \right)} - \pi$$
Or
$$x = 2 \pi n + \operatorname{acos}{\left(w \right)}$$
$$x = 2 \pi n + \operatorname{acos}{\left(w \right)} - \pi$$
, where n - is a integer
substitute w:
$$x_{1} = 2 \pi n + \operatorname{acos}{\left(w_{1} \right)}$$
$$x_{1} = 2 \pi n + \operatorname{acos}{\left(\frac{\sqrt{3}}{2} \right)}$$
$$x_{1} = 2 \pi n + \frac{\pi}{6}$$
$$x_{2} = 2 \pi n + \operatorname{acos}{\left(w_{2} \right)}$$
$$x_{2} = 2 \pi n + \operatorname{acos}{\left(- \frac{\sqrt{3}}{2} \right)}$$
$$x_{2} = 2 \pi n + \frac{5 \pi}{6}$$
$$x_{3} = 2 \pi n + \operatorname{acos}{\left(w_{1} \right)} - \pi$$
$$x_{3} = 2 \pi n - \pi + \operatorname{acos}{\left(\frac{\sqrt{3}}{2} \right)}$$
$$x_{3} = 2 \pi n - \frac{5 \pi}{6}$$
$$x_{4} = 2 \pi n + \operatorname{acos}{\left(w_{2} \right)} - \pi$$
$$x_{4} = 2 \pi n - \pi + \operatorname{acos}{\left(- \frac{\sqrt{3}}{2} \right)}$$
$$x_{4} = 2 \pi n - \frac{\pi}{6}$$
Rapid solution
[src]
pi
x_1 = --
6
$$x_{1} = \frac{\pi}{6}$$
5*pi
x_2 = ----
6
$$x_{2} = \frac{5 \pi}{6}$$
7*pi
x_3 = ----
6
$$x_{3} = \frac{7 \pi}{6}$$
11*pi
x_4 = -----
6
$$x_{4} = \frac{11 \pi}{6}$$
Sum and product of roots
[src]
sum
pi 5*pi 7*pi 11*pi -- + ---- + ---- + ----- 6 6 6 6
$$\left(\frac{\pi}{6}\right) + \left(\frac{5 \pi}{6}\right) + \left(\frac{7 \pi}{6}\right) + \left(\frac{11 \pi}{6}\right)$$
=
4*pi
$$4 \pi$$
product
pi 5*pi 7*pi 11*pi -- * ---- * ---- * ----- 6 6 6 6
$$\left(\frac{\pi}{6}\right) * \left(\frac{5 \pi}{6}\right) * \left(\frac{7 \pi}{6}\right) * \left(\frac{11 \pi}{6}\right)$$
=
4 385*pi ------- 1296
$$\frac{385 \pi^{4}}{1296}$$
Numerical answer
[src]
x1 = 69.6386371545737
x2 = -27.7507351067098
x3 = -5.75958653158129
x4 = -40.317105721069
x5 = 84.2994028713261
x6 = -91.6297857297023
x7 = 5.75958653158129
x8 = -217.293491873294
x9 = -69.6386371545737
x10 = -63.3554518473942
x11 = -78.0162175641465
x12 = 66.497044500984
x13 = -84.2994028713261
x14 = -9.94837673636768
x15 = 71.733032256967
x16 = 44.5058959258554
x17 = 56.025068989018
x18 = 30.8923277602996
x19 = -100.007366139275
x20 = 97.9129710368819
x21 = -81.1578102177363
x22 = -38.2227106186758
x23 = 78.0162175641465
x24 = 41.3643032722656
x25 = 68.5914396033772
x26 = -53.9306738866248
x27 = -16.2315620435473
x28 = -24.60914245312
x29 = 40.317105721069
x30 = -56.025068989018
x31 = 63.3554518473942
x32 = -97.9129710368819
x33 = -68.5914396033772
x34 = 27.7507351067098
x35 = 131.423292675173
x36 = 52.8834763354282
x37 = 9.94837673636768
x38 = -43.4586983746588
x39 = 24.60914245312
x40 = -13.0899693899575
x41 = 12.0427718387609
x42 = 96.8657734856853
x43 = -75.9218224617533
x44 = 0.523598775598299
x45 = -2686.58531759487
x46 = -25.6563400043166
x47 = -12.0427718387609
x48 = -46.6002910282486
x49 = 49.7418836818384
x50 = 85.3466004225227
x51 = 47.6474885794452
x52 = -19.3731546971371
x53 = -90.5825881785057
x54 = -313.635666583381
x55 = -93.7241808320955
x56 = 82.2050077689329
x57 = -71.733032256967
x58 = 18.3259571459405
x59 = -2.61799387799149
x60 = -31.9395253114962
x61 = 3.66519142918809
x62 = -47.6474885794452
x63 = 90.5825881785057
x64 = -41.3643032722656
x65 = 16.2315620435473
x66 = 53.9306738866248
x67 = -3.66519142918809
x68 = -65.4498469497874
x69 = 88.4881930761125
x70 = -62.3082542961976
x71 = -85.3466004225227
x72 = -60.2138591938044
x73 = 34.0339204138894
x74 = 74.8746249105567
x75 = -34.0339204138894
x76 = -35.081117965086
x77 = -21.4675497995303
x78 = 125.140107367993
x79 = 8.90117918517108
x80 = 2.61799387799149
x81 = -87.4409955249159
x82 = -49.7418836818384
x83 = -82.2050077689329
x84 = 91.6297857297023
x85 = 100.007366139275
x86 = 60.2138591938044
x87 = 31.9395253114962
x88 = 38.2227106186758
x89 = 62.3082542961976
x90 = 19.3731546971371
x91 = 75.9218224617533
x92 = -18.3259571459405
x93 = 25.6563400043166
x94 = 93.7241808320955
x95 = 46.6002910282486
x96 = 22.5147473507269
x96 = 22.5147473507269
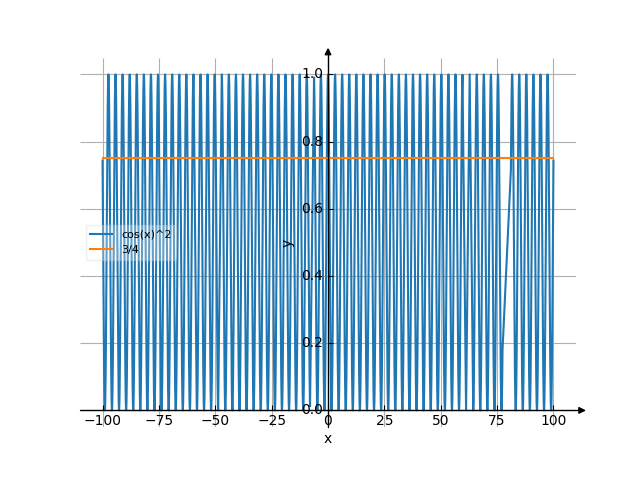
The graph