Mister Exam
Other calculators
-
How to use it?
- Equation:
-
Equation 2^2-x-1=x^2-5*x-(-1-x^2)
-
Equation cos(x)=-1
-
Equation cos(x/3)=0
- Equation tan(x/3)=-(√3/3)
- Express {x} in terms of y where:
- 16*x-17*y=-9
- 10*x-16*y=6
- 4*x-15*y=19
- 7*x-2*y=20
- Integral of d{x}:
-
cos(x/3)
- Limit of the function:
-
cos(x/3)
- Derivative of:
-
cos(x/3)
-
Identical expressions
- cos(x/ three)= zero
- co sinus of e of (x divide by 3) equally 0
- co sinus of e of (x divide by three) equally zero
- cosx/3=0
- cos(x/3)=O
- cos(x divide by 3)=0
-
Similar expressions
- cos(x/3-pi/4)=1/2
- y=acosx/3
- cos((x)/(3)+(2\pi)/(3))=(\sqrt(2))/(2)
- cos(x/3+pi/4)=-√2/2
cos(x/3)=0 equation
The teacher will be very surprised to see your correct solution 😉
The solution
Detail solution
Given the equation
$$\cos{\left(\frac{x}{3} \right)} = 0$$
- this is the simplest trigonometric equation
We get:
$$\cos{\left(\frac{x}{3} \right)} = 0$$
This equation is transformed to
$$\frac{x}{3} = \pi n + \operatorname{acos}{\left(0 \right)}$$
$$\frac{x}{3} = \pi n - \pi + \operatorname{acos}{\left(0 \right)}$$
Or
$$\frac{x}{3} = \pi n + \frac{\pi}{2}$$
$$\frac{x}{3} = \pi n - \frac{\pi}{2}$$
, where n - is a integer
Divide both parts of the equation by
$$\frac{1}{3}$$
we get the answer:
$$x_{1} = 3 \pi n + \frac{3 \pi}{2}$$
$$x_{2} = 3 \pi n - \frac{3 \pi}{2}$$
$$\cos{\left(\frac{x}{3} \right)} = 0$$
- this is the simplest trigonometric equation
with the change of sign in 0
We get:
$$\cos{\left(\frac{x}{3} \right)} = 0$$
This equation is transformed to
$$\frac{x}{3} = \pi n + \operatorname{acos}{\left(0 \right)}$$
$$\frac{x}{3} = \pi n - \pi + \operatorname{acos}{\left(0 \right)}$$
Or
$$\frac{x}{3} = \pi n + \frac{\pi}{2}$$
$$\frac{x}{3} = \pi n - \frac{\pi}{2}$$
, where n - is a integer
Divide both parts of the equation by
$$\frac{1}{3}$$
we get the answer:
$$x_{1} = 3 \pi n + \frac{3 \pi}{2}$$
$$x_{2} = 3 \pi n - \frac{3 \pi}{2}$$
Rapid solution
[src]
3*pi
x1 = ----
2
$$x_{1} = \frac{3 \pi}{2}$$
9*pi
x2 = ----
2
$$x_{2} = \frac{9 \pi}{2}$$
x2 = 9*pi/2
Sum and product of roots
[src]
sum
3*pi 9*pi ---- + ---- 2 2
$$\frac{3 \pi}{2} + \frac{9 \pi}{2}$$
=
6*pi
$$6 \pi$$
product
3*pi 9*pi ----*---- 2 2
$$\frac{3 \pi}{2} \frac{9 \pi}{2}$$
=
2 27*pi ------ 4
$$\frac{27 \pi^{2}}{4}$$
27*pi^2/4
Numerical answer
[src]
x1 = -70.6858347057703
x2 = -4.71238898038469
x3 = 2653.07499595658
x4 = 42.4115008234622
x5 = -23.5619449019235
x6 = -61.261056745001
x7 = -89.5353906273091
x8 = -249.756615960389
x9 = -32.9867228626928
x10 = 61.261056745001
x11 = -42.4115008234622
x12 = -51.8362787842316
x13 = 32.9867228626928
x14 = 98.9601685880785
x15 = 70.6858347057703
x16 = -14.1371669411541
x17 = -80.1106126665397
x18 = -4867.89781673738
x19 = 23.5619449019235
x20 = 51.8362787842316
x21 = 80.1106126665397
x22 = 155.508836352695
x23 = 4.71238898038469
x24 = 14.1371669411541
x25 = 5659.57916544201
x26 = -98.9601685880785
x27 = 89.5353906273091
x27 = 89.5353906273091
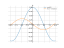
The graph