Derivative of y=arcsinx^2
The solution
The second derivative
[src]
/ 1 x*asin(x) \ 2*|- ------- + -----------| | 2 3/2| | -1 + x / 2\ | \ \1 - x / /
The third derivative
[src]
/ 2 \ | asin(x) 3*x 3*x *asin(x)| 2*|----------- + ---------- + ------------| | 3/2 2 5/2 | |/ 2\ / 2\ / 2\ | \\1 - x / \-1 + x / \1 - x / /
The graph
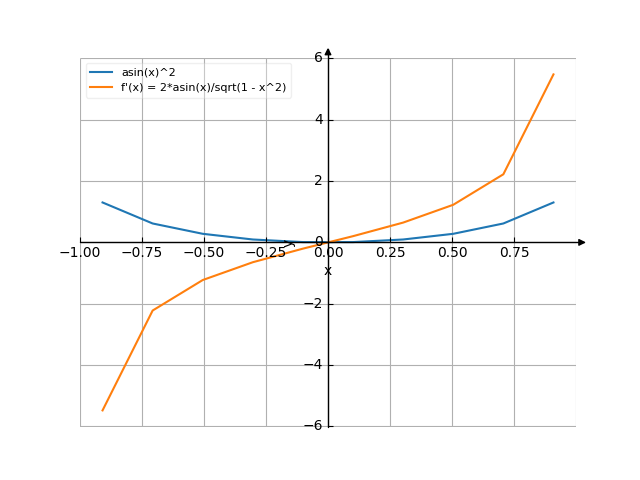

![Find the derivative of y' = f'(x) = y=arcsinx² (y equally arc sinus of x squared) - functions. Find the derivative of the function at the point. [THERE'S THE ANSWER!] y=arcsinx^2](/media/krcore-image-pods/176/hash/derivative/a/a5/18e99af4c549675fb663af866f6a5.png)
 Derivative of 2*sinh(x)*cosh(x)
Derivative of 2*sinh(x)*cosh(x)
 Derivative of (x-2)^4
Derivative of (x-2)^4
 Derivative of (x^2-1)*(x^4+2)
Derivative of (x^2-1)*(x^4+2)
 Derivative of log(e)
Derivative of log(e)
 arcsinx^2
arcsinx^2