Mister Exam

Other calculators

(arcsin(x^2))/ln(3x)
The derivative of the function/ (arcsin(x^2))/ln(3x)

You entered:

(arcsin(x^2))/ln(3x)

What you mean?

asin(x^2)/log(3*x)
 
asin(x^2)/((log(3)*x))
 
asin(x^2)*3*x/log(x)
 
asin(x^2)/log(3*x)
 
asin(x^2)/((log(3)*x))
 
asin(x^2)*3*x/log(x)
 
asin(x^2)*3*x/log(x)

Derivative of (arcsin(x^2))/ln(3x)

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
    / 2\
asin\x /
--------
log(3*x)
asin⁡(x2)log⁡(3x)\frac{\operatorname{asin}{\left(x^{2} \right)}}{\log{\left(3 x \right)}} 
  /    / 2\\
d |asin\x /|
--|--------|
dx\log(3*x)/
ddxasin⁡(x2)log⁡(3x)\frac{d}{d x} \frac{\operatorname{asin}{\left(x^{2} \right)}}{\log{\left(3 x \right)}}
Transform
The graph
02468-8-6-4-2-1010-5050
Plot the graph f(x)
Plot the graph f'(x)
The first derivative [src] 
        / 2\                        
    asin\x /            2*x         
- ----------- + --------------------
       2           ________         
  x*log (3*x)     /      4          
                \/  1 - x  *log(3*x)
2x1−x4log⁡(3x)−asin⁡(x2)xlog⁡(3x)2\frac{2 x}{\sqrt{1 - x^{4}} \log{\left(3 x \right)}} - \frac{\operatorname{asin}{\left(x^{2} \right)}}{x \log{\left(3 x \right)}^{2}}
Simplify
The second derivative [src] 
                           /          4 \                          
                           |       2*x  |                          
                         2*|-1 + -------|   /       2    \     / 2\
                           |           4|   |1 + --------|*asin\x /
           4               \     -1 + x /   \    log(3*x)/         
- -------------------- - ---------------- + -----------------------
     ________                 ________             2               
    /      4                 /      4             x *log(3*x)      
  \/  1 - x  *log(3*x)     \/  1 - x                               
-------------------------------------------------------------------
                              log(3*x)
−2⋅(2x4x4−1−1)1−x4−41−x4log⁡(3x)+(1+2log⁡(3x))asin⁡(x2)x2log⁡(3x)log⁡(3x)\frac{- \frac{2 \cdot \left(\frac{2 x^{4}}{x^{4} - 1} - 1\right)}{\sqrt{1 - x^{4}}} - \frac{4}{\sqrt{1 - x^{4}} \log{\left(3 x \right)}} + \frac{\left(1 + \frac{2}{\log{\left(3 x \right)}}\right) \operatorname{asin}{\left(x^{2} \right)}}{x^{2} \log{\left(3 x \right)}}}{\log{\left(3 x \right)}}
Simplify
The third derivative [src] 
  /       /          4 \                                                                       /          4 \   \
  |     3 |       6*x  |   /       3           3    \     / 2\                                 |       2*x  |   |
  |  2*x *|-5 + -------|   |1 + -------- + ---------|*asin\x /        /       2    \         3*|-1 + -------|   |
  |       |           4|   |    log(3*x)      2     |               3*|1 + --------|           |           4|   |
  |       \     -1 + x /   \               log (3*x)/                 \    log(3*x)/           \     -1 + x /   |
2*|- ------------------- - ----------------------------------- + ---------------------- + ----------------------|
  |              3/2                    3                             ________                 ________         |
  |      /     4\                      x *log(3*x)                   /      4                 /      4          |
  \      \1 - x /                                                x*\/  1 - x  *log(3*x)   x*\/  1 - x  *log(3*x)/
-----------------------------------------------------------------------------------------------------------------
                                                     log(3*x)
2(−2x3⋅(6x4x4−1−5)(1−x4)32+3⋅(1+2log⁡(3x))x1−x4log⁡(3x)+3⋅(2x4x4−1−1)x1−x4log⁡(3x)−(1+3log⁡(3x)+3log⁡(3x)2)asin⁡(x2)x3log⁡(3x))log⁡(3x)\frac{2 \left(- \frac{2 x^{3} \cdot \left(\frac{6 x^{4}}{x^{4} - 1} - 5\right)}{\left(1 - x^{4}\right)^{\frac{3}{2}}} + \frac{3 \cdot \left(1 + \frac{2}{\log{\left(3 x \right)}}\right)}{x \sqrt{1 - x^{4}} \log{\left(3 x \right)}} + \frac{3 \cdot \left(\frac{2 x^{4}}{x^{4} - 1} - 1\right)}{x \sqrt{1 - x^{4}} \log{\left(3 x \right)}} - \frac{\left(1 + \frac{3}{\log{\left(3 x \right)}} + \frac{3}{\log{\left(3 x \right)}^{2}}\right) \operatorname{asin}{\left(x^{2} \right)}}{x^{3} \log{\left(3 x \right)}}\right)}{\log{\left(3 x \right)}}
Simplify
The graph
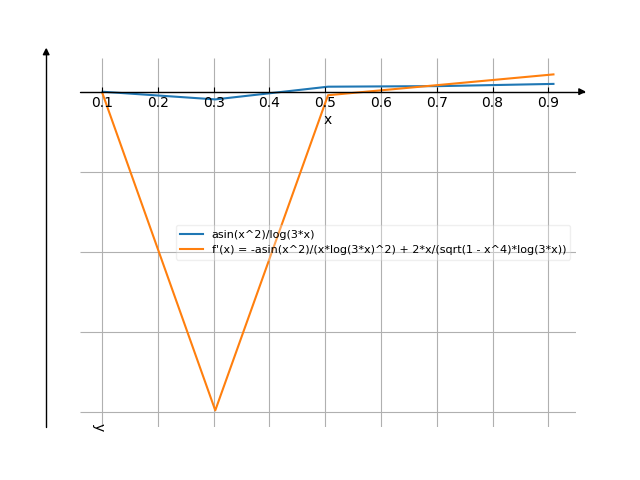
Derivative of (arcsin(x^2))/ln(3x)
    © Mister Exam – Calculator