Mister Exam

Lang:

Other calculators

How to use it?
Derivative of:
Derivative of e^(2*cos(t)^(2)-2*sin(t)^(2))
Derivative of 2^x+1
Derivative of x^2+2x
Derivative of (x^2-1)/x
Identical expressions
(x^ three + four)^tan(x/ two)
(x cubed plus 4) to the power of tangent of (x divide by 2)
(x to the power of three plus four) to the power of tangent of (x divide by two)
(x3+4)tan(x/2)
x3+4tanx/2
(x³+4)^tan(x/2)
(x to the power of 3+4) to the power of tan(x/2)
x^3+4^tanx/2
(x^3+4)^tan(x divide by 2)
Similar expressions
(x^3-4)^tan(x/2)

The derivative of the function/ (x^3+4)^tan(x/2)

Derivative of (x^3+4)^tan(x/2)

The solution

You have entered [src]

           /x\
        tan|-|
           \2/
/ 3    \      
\x  + 4/

\left(x^{3} + 4\right)^{\tan{\left(\frac{x}{2} \right)}}

  /           /x\\
  |        tan|-||
  |           \2/|
d |/ 3    \      |
--\\x  + 4/      /
dx

\frac{d}{d x} \left(x^{3} + 4\right)^{\tan{\left(\frac{x}{2} \right)}}

Transform

Detail solution

Don't know the steps in finding this derivative.

But the derivative is

$\left(\log{\left(\tan{\left(\frac{x}{2} \right)} \right)} + 1\right) \tan^{\tan{\left(\frac{x}{2} \right)}}{\left(\frac{x}{2} \right)}$
Now simplify:

$\left(\log{\left(\tan{\left(\frac{x}{2} \right)} \right)} + 1\right) \tan^{\tan{\left(\frac{x}{2} \right)}}{\left(\frac{x}{2} \right)}$

The answer is:

\left(\log{\left(\tan{\left(\frac{x}{2} \right)} \right)} + 1\right) \tan^{\tan{\left(\frac{x}{2} \right)}}{\left(\frac{x}{2} \right)}

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

           /x\                                          
        tan|-| //       2/x\\                  2    /x\\
           \2/ ||    tan |-||               3*x *tan|-||
/ 3    \       ||1       \2/|    / 3    \           \2/|
\x  + 4/      *||- + -------|*log\x  + 4/ + -----------|
               |\2      2   /                   3      |
               \                               x  + 4  /

\left(x^{3} + 4\right)^{\tan{\left(\frac{x}{2} \right)}} \left(\frac{3 x^{2} \tan{\left(\frac{x}{2} \right)}}{x^{3} + 4} + \left(\frac{\tan^{2}{\left(\frac{x}{2} \right)}}{2} + \frac{1}{2}\right) \log{\left(x^{3} + 4 \right)}\right)

Simplify

The second derivative [src]

               /                                         2                                                                                   \
               |/                               2    /x\\                                                                                    |
               ||                            6*x *tan|-||                                                                                    |
           /x\ ||/       2/x\\    /     3\           \2/|                                                                                    |
        tan|-| |||1 + tan |-||*log\4 + x / + -----------|    /       2/x\\    /     3\    /x\      4    /x\      2 /       2/x\\          /x\|
           \2/ ||\        \2//                       3  |    |1 + tan |-||*log\4 + x /*tan|-|   9*x *tan|-|   3*x *|1 + tan |-||   6*x*tan|-||
/     3\       |\                               4 + x   /    \        \2//                \2/           \2/        \        \2//          \2/|
\4 + x /      *|------------------------------------------ + -------------------------------- - ----------- + ------------------ + ----------|
               |                    4                                       2                            2               3                3  |
               |                                                                                 /     3\           4 + x            4 + x   |
               \                                                                                 \4 + x /                                    /

\left(x^{3} + 4\right)^{\tan{\left(\frac{x}{2} \right)}} \left(- \frac{9 x^{4} \tan{\left(\frac{x}{2} \right)}}{\left(x^{3} + 4\right)^{2}} + \frac{\left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right) \log{\left(x^{3} + 4 \right)} \tan{\left(\frac{x}{2} \right)}}{2} + \frac{3 x^{2} \left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right)}{x^{3} + 4} + \frac{\left(\frac{6 x^{2} \tan{\left(\frac{x}{2} \right)}}{x^{3} + 4} + \left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right) \log{\left(x^{3} + 4 \right)}\right)^{2}}{4} + \frac{6 x \tan{\left(\frac{x}{2} \right)}}{x^{3} + 4}\right)

Simplify

The third derivative [src]

               /                                         3                                             /                               2    /x\\ /                                       4    /x\      2 /       2/x\\           /x\\                                                                                                                                        \
               |/                               2    /x\\                                              |                            6*x *tan|-|| |                                   18*x *tan|-|   6*x *|1 + tan |-||   12*x*tan|-||                                                                                                                                        |
               ||                            6*x *tan|-||                                              |/       2/x\\    /     3\           \2/| |/       2/x\\    /     3\    /x\            \2/        \        \2//           \2/|                                                                                                                                        |
           /x\ ||/       2/x\\    /     3\           \2/|                            2               3*||1 + tan |-||*log\4 + x / + -----------|*||1 + tan |-||*log\4 + x /*tan|-| - ------------ + ------------------ + -----------|                                                                                                                                        |
        tan|-| |||1 + tan |-||*log\4 + x / + -----------|         /x\   /       2/x\\     /     3\     |\        \2//                       3  | |\        \2//                \2/            2                3                 3  |      2/x\ /       2/x\\    /     3\       3    /x\       /       2/x\\       6    /x\       4 /       2/x\\      2 /       2/x\\    /x\|
           \2/ ||\        \2//                       3  |    6*tan|-|   |1 + tan |-|| *log\4 + x /     \                               4 + x   / |                                    /     3\            4 + x             4 + x   |   tan |-|*|1 + tan |-||*log\4 + x /   54*x *tan|-|   9*x*|1 + tan |-||   54*x *tan|-|   27*x *|1 + tan |-||   9*x *|1 + tan |-||*tan|-||
/     3\       |\                               4 + x   /         \2/   \        \2//                                                            \                                    \4 + x /                                      /       \2/ \        \2//                        \2/       \        \2//            \2/         \        \2//        \        \2//    \2/|
\4 + x /      *|------------------------------------------ + -------- + -------------------------- + -------------------------------------------------------------------------------------------------------------------------------- + --------------------------------- - ------------ + ----------------- + ------------ - ------------------- + -------------------------|
               |                    8                              3                4                                                                               4                                                                                   2                            2                3                 3                   2                 /     3\       |
               |                                              4 + x                                                                                                                                                                                                          /     3\            4 + x          /     3\            /     3\                2*\4 + x /       |
               \                                                                                                                                                                                                                                                             \4 + x /                           \4 + x /          2*\4 + x /                                 /

\left(x^{3} + 4\right)^{\tan{\left(\frac{x}{2} \right)}} \left(\frac{54 x^{6} \tan{\left(\frac{x}{2} \right)}}{\left(x^{3} + 4\right)^{3}} + \frac{\left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right) \log{\left(x^{3} + 4 \right)} \tan^{2}{\left(\frac{x}{2} \right)}}{2} - \frac{27 x^{4} \left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right)}{2 \left(x^{3} + 4\right)^{2}} + \frac{9 x^{2} \left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right) \tan{\left(\frac{x}{2} \right)}}{2 \left(x^{3} + 4\right)} + \frac{\left(\frac{6 x^{2} \tan{\left(\frac{x}{2} \right)}}{x^{3} + 4} + \left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right) \log{\left(x^{3} + 4 \right)}\right)^{3}}{8} + \frac{\left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right)^{2} \log{\left(x^{3} + 4 \right)}}{4} - \frac{54 x^{3} \tan{\left(\frac{x}{2} \right)}}{\left(x^{3} + 4\right)^{2}} + \frac{3 \cdot \left(\frac{6 x^{2} \tan{\left(\frac{x}{2} \right)}}{x^{3} + 4} + \left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right) \log{\left(x^{3} + 4 \right)}\right) \left(- \frac{18 x^{4} \tan{\left(\frac{x}{2} \right)}}{\left(x^{3} + 4\right)^{2}} + \left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right) \log{\left(x^{3} + 4 \right)} \tan{\left(\frac{x}{2} \right)} + \frac{6 x^{2} \left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right)}{x^{3} + 4} + \frac{12 x \tan{\left(\frac{x}{2} \right)}}{x^{3} + 4}\right)}{4} + \frac{9 x \left(\tan^{2}{\left(\frac{x}{2} \right)} + 1\right)}{x^{3} + 4} + \frac{6 \tan{\left(\frac{x}{2} \right)}}{x^{3} + 4}\right)

Simplify

The graph

Other calculators

How to use it?

Identical expressions

Similar expressions

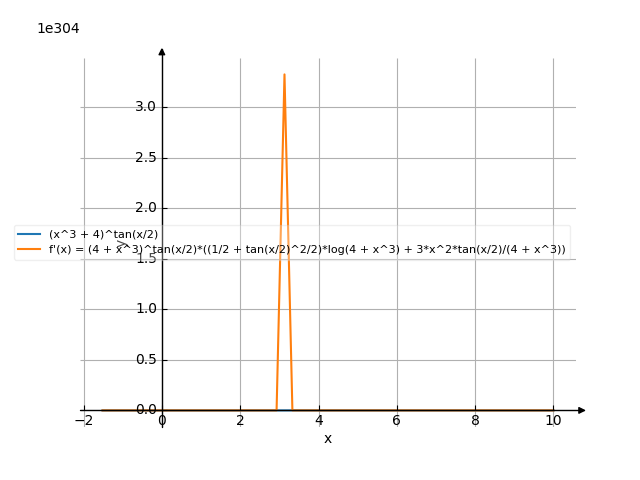
Derivative of (x^3+4)^tan(x/2)

The graph:

Piecewise:

The solution