Mister Exam

Lang:

The derivative of the function/ xsqrt(x+1)

Derivative of xsqrt(x+1)

The solution

You have entered [src]

    _______
x*\/ x + 1

$$x \sqrt{x + 1}$$

x*sqrt(x + 1)

Detail solution

Apply the product rule:

$\frac{d}{d x} f{\left(x \right)} g{\left(x \right)} = f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}$

$f{\left(x \right)} = x$ ; to find $\frac{d}{d x} f{\left(x \right)}$ :
1. Apply the power rule: $x$ goes to $1$
$g{\left(x \right)} = \sqrt{x + 1}$ ; to find $\frac{d}{d x} g{\left(x \right)}$ :
1. Let $u = x + 1$ .
2. Apply the power rule: $\sqrt{u}$ goes to $\frac{1}{2 \sqrt{u}}$
3. Then, apply the chain rule. Multiply by $\frac{d}{d x} \left(x + 1\right)$ :
  1. Differentiate $x + 1$ term by term:
    1. Apply the power rule: $x$ goes to $1$
    2. The derivative of the constant $1$ is zero.
    The result is: $1$
  The result of the chain rule is:
  
  $\frac{1}{2 \sqrt{x + 1}}$
The result is: $\frac{x}{2 \sqrt{x + 1}} + \sqrt{x + 1}$
Now simplify:

$\frac{3 x + 2}{2 \sqrt{x + 1}}$

The answer is:

$\frac{3 x + 2}{2 \sqrt{x + 1}}$

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

  _______        x     
\/ x + 1  + -----------
                _______
            2*\/ x + 1

$$\frac{x}{2 \sqrt{x + 1}} + \sqrt{x + 1}$$

Simplify

The second derivative [src]

        x    
1 - ---------
    4*(1 + x)
-------------
    _______  
  \/ 1 + x

$$\frac{- \frac{x}{4 \left(x + 1\right)} + 1}{\sqrt{x + 1}}$$

Simplify

The third derivative [src]

  /       x  \
3*|-2 + -----|
  \     1 + x/
--------------
          3/2 
 8*(1 + x)

$$\frac{3 \left(\frac{x}{x + 1} - 2\right)}{8 \left(x + 1\right)^{\frac{3}{2}}}$$

Simplify

The graph

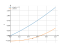Derivative of xsqrt(x+1)