Mister Exam

Lang:

The derivative of the function/ x*sqrt(x)-3*x+1

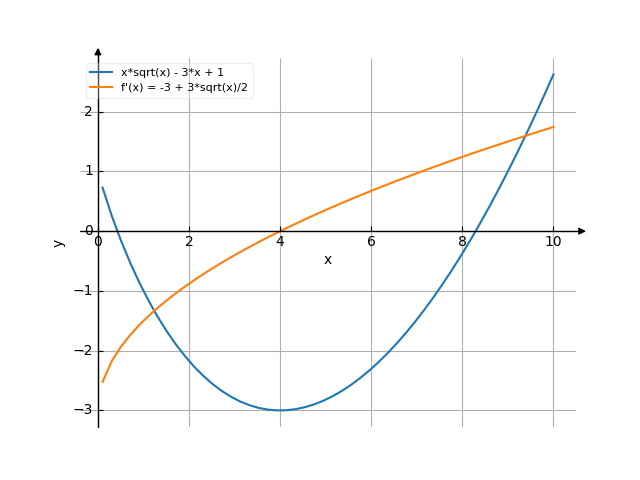
Derivative of xsqrt(x)-3x+1

The solution

You have entered [src]

    ___          
x*\/ x  - 3*x + 1

$$\sqrt{x} x - 3 x + 1$$

d /    ___          \
--\x*\/ x  - 3*x + 1/
dx

$$\frac{d}{d x} \left(\sqrt{x} x - 3 x + 1\right)$$

Transform

Detail solution

Differentiate $\sqrt{x} x - 3 x + 1$ term by term:
1. Apply the product rule:
  
  $\frac{d}{d x} f{\left(x \right)} g{\left(x \right)} = f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}$
  
  $f{\left(x \right)} = x$ ; to find $\frac{d}{d x} f{\left(x \right)}$ :
  1. Apply the power rule: $x$ goes to $1$
  $g{\left(x \right)} = \sqrt{x}$ ; to find $\frac{d}{d x} g{\left(x \right)}$ :
  1. Apply the power rule: $\sqrt{x}$ goes to $\frac{1}{2 \sqrt{x}}$
  The result is: $\frac{3 \sqrt{x}}{2}$
2. The derivative of a constant times a function is the constant times the derivative of the function.
  1. The derivative of a constant times a function is the constant times the derivative of the function.
    1. Apply the power rule: $x$ goes to $1$
    So, the result is: $3$
  So, the result is: $-3$
3. The derivative of the constant $1$ is zero.
The result is: $\frac{3 \sqrt{x}}{2} - 3$

The answer is:

$\frac{3 \sqrt{x}}{2} - 3$

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

         ___
     3*\/ x 
-3 + -------
        2

$$\frac{3 \sqrt{x}}{2} - 3$$

Simplify

The second derivative [src]

   3   
-------
    ___
4*\/ x

$$\frac{3}{4 \sqrt{x}}$$

Simplify

The third derivative [src]

 -3   
------
   3/2
8*x

$$- \frac{3}{8 x^{\frac{3}{2}}}$$

Simplify

The graph

Derivative of x*sqrt(x)-3*x+1