Derivative of sqrt(x)*exp(x)

You have entered [src]

  ___  x
\/ x *e

$$\sqrt{x} e^{x}$$

sqrt(x)*exp(x)

Detail solution

Apply the product rule:

$\frac{d}{d x} f{\left(x \right)} g{\left(x \right)} = f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}$

$f{\left(x \right)} = \sqrt{x}$ ; to find $\frac{d}{d x} f{\left(x \right)}$ :
1. Apply the power rule: $\sqrt{x}$ goes to $\frac{1}{2 \sqrt{x}}$
$g{\left(x \right)} = e^{x}$ ; to find $\frac{d}{d x} g{\left(x \right)}$ :
1. The derivative of $e^{x}$ is itself.
The result is: $\sqrt{x} e^{x} + \frac{e^{x}}{2 \sqrt{x}}$
Now simplify:

$\frac{\left(x + \frac{1}{2}\right) e^{x}}{\sqrt{x}}$

The answer is:

$\frac{\left(x + \frac{1}{2}\right) e^{x}}{\sqrt{x}}$

The graph

Plot the graph f(x)

Plot the graph f'(x)

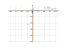
The first derivative [src]

               x  
  ___  x      e   
\/ x *e  + -------
               ___
           2*\/ x

$$\sqrt{x} e^{x} + \frac{e^{x}}{2 \sqrt{x}}$$

Simplify

The second derivative [src]

/  ___     1       1   \  x
|\/ x  + ----- - ------|*e 
|          ___      3/2|   
\        \/ x    4*x   /

$$\left(\sqrt{x} + \frac{1}{\sqrt{x}} - \frac{1}{4 x^{\frac{3}{2}}}\right) e^{x}$$

Simplify

The third derivative [src]

/  ___     3         3        3   \  x
|\/ x  - ------ + ------- + ------|*e 
|           3/2       ___      5/2|   
\        4*x      2*\/ x    8*x   /

$$\left(\sqrt{x} + \frac{3}{2 \sqrt{x}} - \frac{3}{4 x^{\frac{3}{2}}} + \frac{3}{8 x^{\frac{5}{2}}}\right) e^{x}$$

Simplify

Other calculators

How to use it?

Identical expressions

Derivative of sqrt(x)*exp(x)

The graph:

Piecewise:

The solution