Mister Exam

Other calculators

sin^-1x
The derivative of the function/ sin^-1x

Derivative of sin^-1x

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
  1   
------
sin(x)
1sin⁡(x)\frac{1}{\sin{\left(x \right)}} 
d /  1   \
--|------|
dx\sin(x)/
ddx1sin⁡(x)\frac{d}{d x} \frac{1}{\sin{\left(x \right)}}
Transform
Detail solution

  1. Let u=sin⁡(x)u = \sin{\left(x \right)}.

  2. Apply the power rule: 1u\frac{1}{u} goes to −1u2- \frac{1}{u^{2}}

  3. Then, apply the chain rule. Multiply by ddxsin⁡(x)\frac{d}{d x} \sin{\left(x \right)}:

    1. The derivative of sine is cosine:

      ddxsin⁡(x)=cos⁡(x)\frac{d}{d x} \sin{\left(x \right)} = \cos{\left(x \right)}

    The result of the chain rule is:

    −cos⁡(x)sin⁡2(x)- \frac{\cos{\left(x \right)}}{\sin^{2}{\left(x \right)}}

The answer is:

−cos⁡(x)sin⁡2(x)- \frac{\cos{\left(x \right)}}{\sin^{2}{\left(x \right)}}

The graph
02468-8-6-4-2-1010-1000010000
Plot the graph f(x)
Plot the graph f'(x)
The first derivative [src] 
-cos(x) 
--------
   2    
sin (x)
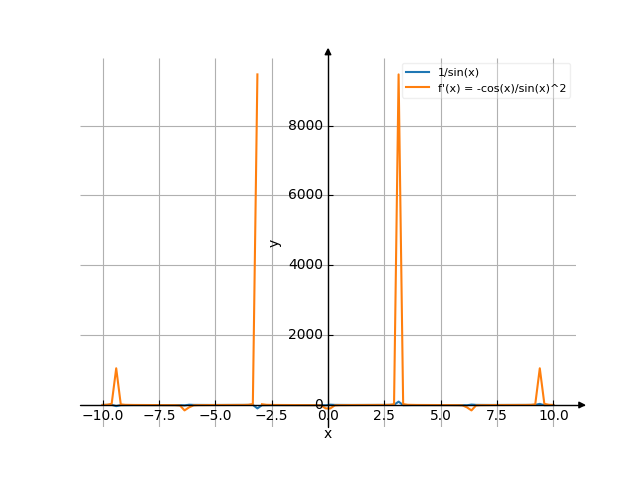
−cos⁡(x)sin⁡2(x)- \frac{\cos{\left(x \right)}}{\sin^{2}{\left(x \right)}}
Simplify
The second derivative [src] 
         2   
    2*cos (x)
1 + ---------
        2    
     sin (x) 
-------------
    sin(x)
1+2cos⁡2(x)sin⁡2(x)sin⁡(x)\frac{1 + \frac{2 \cos^{2}{\left(x \right)}}{\sin^{2}{\left(x \right)}}}{\sin{\left(x \right)}}
Simplify
The third derivative [src] 
 /         2   \        
 |    6*cos (x)|        
-|5 + ---------|*cos(x) 
 |        2    |        
 \     sin (x) /        
------------------------
           2            
        sin (x)
−(5+6cos⁡2(x)sin⁡2(x))cos⁡(x)sin⁡2(x)- \frac{\left(5 + \frac{6 \cos^{2}{\left(x \right)}}{\sin^{2}{\left(x \right)}}\right) \cos{\left(x \right)}}{\sin^{2}{\left(x \right)}}
Simplify
The graph
Derivative of sin^-1x
    © Mister Exam – Calculator