Mister Exam

Lang:

Other calculators

How to use it?
Derivative of:
Derivative of 5x
Derivative of 5x^3
Derivative of x*cos(2*x)
Derivative of x^2+2x
Identical expressions
(ln^7x+ctg5x)^ ten
(ln to the power of 7x plus ctg5x) to the power of 10
(ln to the power of 7x plus ctg5x) to the power of ten
(ln7x+ctg5x)10
ln7x+ctg5x10
(ln⁷x+ctg5x)^10
ln^7x+ctg5x^10
Similar expressions
(ln^7x-ctg5x)^10

The derivative of the function/ (ln^7x+ctg5x)^10

Derivative of (ln^7x+ctg5x)^10

The solution

You have entered [src]

                    10
/   7              \  
\log (x) + cot(5*x)/

$$\left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right)^{10}$$

  /                    10\
d |/   7              \  |
--\\log (x) + cot(5*x)/  /
dx

$$\frac{d}{d x} \left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right)^{10}$$

Transform

Detail solution

Let $u = \log{\left(x \right)}^{7} + \cot{\left(5 x \right)}$ .
Apply the power rule: $u^{10}$ goes to $10 u^{9}$
Then, apply the chain rule. Multiply by $\frac{d}{d x} \left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right)$ :
1. Differentiate $\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}$ term by term:
  1. Let $u = \log{\left(x \right)}$ .
  2. Apply the power rule: $u^{7}$ goes to $7 u^{6}$
  3. Then, apply the chain rule. Multiply by $\frac{d}{d x} \log{\left(x \right)}$ :
    1. The derivative of $\log{\left(x \right)}$ is $\frac{1}{x}$ .
    The result of the chain rule is:
    
    $\frac{7 \log{\left(x \right)}^{6}}{x}$
  4. There are multiple ways to do this derivative.
    Method #1
    1. Rewrite the function to be differentiated:
      
      $\cot{\left(5 x \right)} = \frac{1}{\tan{\left(5 x \right)}}$
    2. Let $u = \tan{\left(5 x \right)}$ .
    3. Apply the power rule: $\frac{1}{u}$ goes to $- \frac{1}{u^{2}}$
    4. Then, apply the chain rule. Multiply by $\frac{d}{d x} \tan{\left(5 x \right)}$ :
      
      Rewrite the function to be differentiated:
      
      $\tan{\left(5 x \right)} = \frac{\sin{\left(5 x \right)}}{\cos{\left(5 x \right)}}$
      
      Apply the quotient rule, which is:
      
      $\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}$
      
      $f{\left(x \right)} = \sin{\left(5 x \right)}$ and $g{\left(x \right)} = \cos{\left(5 x \right)}$ .
      
      To find $\frac{d}{d x} f{\left(x \right)}$ :
      
      Let $u = 5 x$ .
      
      The derivative of sine is cosine:
      
      $\frac{d}{d u} \sin{\left(u \right)} = \cos{\left(u \right)}$
      
      Then, apply the chain rule. Multiply by $\frac{d}{d x} 5 x$ :
      
      The derivative of a constant times a function is the constant times the derivative of the function.
      
      Apply the power rule: $x$ goes to $1$
      
      So, the result is: $5$
      
      The result of the chain rule is:
      
      $5 \cos{\left(5 x \right)}$
      
      To find $\frac{d}{d x} g{\left(x \right)}$ :
      
      Let $u = 5 x$ .
      
      The derivative of cosine is negative sine:
      
      $\frac{d}{d u} \cos{\left(u \right)} = - \sin{\left(u \right)}$
      
      Then, apply the chain rule. Multiply by $\frac{d}{d x} 5 x$ :
      
      The derivative of a constant times a function is the constant times the derivative of the function.
      
      Apply the power rule: $x$ goes to $1$
      
      So, the result is: $5$
      
      The result of the chain rule is:
      
      $- 5 \sin{\left(5 x \right)}$
      
      Now plug in to the quotient rule:
      
      $\frac{5 \sin^{2}{\left(5 x \right)} + 5 \cos^{2}{\left(5 x \right)}}{\cos^{2}{\left(5 x \right)}}$
      
      The result of the chain rule is:
      
      $- \frac{5 \sin^{2}{\left(5 x \right)} + 5 \cos^{2}{\left(5 x \right)}}{\cos^{2}{\left(5 x \right)} \tan^{2}{\left(5 x \right)}}$
    Method #2
    1. Rewrite the function to be differentiated:
      
      $\cot{\left(5 x \right)} = \frac{\cos{\left(5 x \right)}}{\sin{\left(5 x \right)}}$
    2. Apply the quotient rule, which is:
      
      $\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}$
      
      $f{\left(x \right)} = \cos{\left(5 x \right)}$ and $g{\left(x \right)} = \sin{\left(5 x \right)}$ .
      
      To find $\frac{d}{d x} f{\left(x \right)}$ :
      
      Let $u = 5 x$ .
      
      The derivative of cosine is negative sine:
      
      $\frac{d}{d u} \cos{\left(u \right)} = - \sin{\left(u \right)}$
      
      Then, apply the chain rule. Multiply by $\frac{d}{d x} 5 x$ :
      
      The derivative of a constant times a function is the constant times the derivative of the function.
      
      Apply the power rule: $x$ goes to $1$
      
      So, the result is: $5$
      
      The result of the chain rule is:
      
      $- 5 \sin{\left(5 x \right)}$
      
      To find $\frac{d}{d x} g{\left(x \right)}$ :
      
      Let $u = 5 x$ .
      
      The derivative of sine is cosine:
      
      $\frac{d}{d u} \sin{\left(u \right)} = \cos{\left(u \right)}$
      
      Then, apply the chain rule. Multiply by $\frac{d}{d x} 5 x$ :
      
      The derivative of a constant times a function is the constant times the derivative of the function.
      
      Apply the power rule: $x$ goes to $1$
      
      So, the result is: $5$
      
      The result of the chain rule is:
      
      $5 \cos{\left(5 x \right)}$
      
      Now plug in to the quotient rule:
      
      $\frac{- 5 \sin^{2}{\left(5 x \right)} - 5 \cos^{2}{\left(5 x \right)}}{\sin^{2}{\left(5 x \right)}}$
  The result is: $- \frac{5 \sin^{2}{\left(5 x \right)} + 5 \cos^{2}{\left(5 x \right)}}{\cos^{2}{\left(5 x \right)} \tan^{2}{\left(5 x \right)}} + \frac{7 \log{\left(x \right)}^{6}}{x}$
The result of the chain rule is:

$10 \left(- \frac{5 \sin^{2}{\left(5 x \right)} + 5 \cos^{2}{\left(5 x \right)}}{\cos^{2}{\left(5 x \right)} \tan^{2}{\left(5 x \right)}} + \frac{7 \log{\left(x \right)}^{6}}{x}\right) \left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right)^{9}$
Now simplify:

$\frac{\left(- 50 x + 70 \log{\left(x \right)}^{6} \sin^{2}{\left(5 x \right)}\right) \left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right)^{9}}{x \cos^{2}{\left(5 x \right)} \tan^{2}{\left(5 x \right)}}$

The answer is:

$\frac{\left(- 50 x + 70 \log{\left(x \right)}^{6} \sin^{2}{\left(5 x \right)}\right) \left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right)^{9}}{x \cos^{2}{\left(5 x \right)} \tan^{2}{\left(5 x \right)}}$

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

                    9 /                           6   \
/   7              \  |            2        70*log (x)|
\log (x) + cot(5*x)/ *|-50 - 50*cot (5*x) + ----------|
                      \                         x     /

$$\left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right)^{9} \left(\frac{70 \log{\left(x \right)}^{6}}{x} - 50 \cot^{2}{\left(5 x \right)} - 50\right)$$

Simplify

The second derivative [src]

                         /                               2                                                                                \
                       8 |  /                       6   \                         /       6            5                                 \|
   /   7              \  |  |         2        7*log (x)|    /   7              \ |  7*log (x)   42*log (x)      /       2     \         ||
10*\log (x) + cot(5*x)/ *|9*|5 + 5*cot (5*x) - ---------|  + \log (x) + cot(5*x)/*|- --------- + ---------- + 50*\1 + cot (5*x)/*cot(5*x)||
                         |  \                      x    /                         |       2           2                                  ||
                         \                                                        \      x           x                                   //

$$10 \left(\left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right) \left(- \frac{7 \log{\left(x \right)}^{6}}{x^{2}} + \frac{42 \log{\left(x \right)}^{5}}{x^{2}} + 50 \left(\cot^{2}{\left(5 x \right)} + 1\right) \cot{\left(5 x \right)}\right) + 9 \left(- \frac{7 \log{\left(x \right)}^{6}}{x} + 5 \cot^{2}{\left(5 x \right)} + 5\right)^{2}\right) \left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right)^{8}$$

Simplify

The third derivative [src]

                          /                                3                                                                                                                                                                                                                                         \
                        7 |   /                       6   \                          2 /                   2          4           6            5                                   \                           /                       6   \ /       6            5                                 \|
    /   7              \  |   |         2        7*log (x)|      /   7              \  |    /       2     \    105*log (x)   7*log (x)   63*log (x)          2      /       2     \|      /   7              \ |         2        7*log (x)| |  7*log (x)   42*log (x)      /       2     \         ||
-10*\log (x) + cot(5*x)/ *|72*|5 + 5*cot (5*x) - ---------|  + 2*\log (x) + cot(5*x)/ *|125*\1 + cot (5*x)/  - ----------- - --------- + ---------- + 250*cot (5*x)*\1 + cot (5*x)/| + 27*\log (x) + cot(5*x)/*|5 + 5*cot (5*x) - ---------|*|- --------- + ---------- + 50*\1 + cot (5*x)/*cot(5*x)||
                          |   \                      x    /                            |                             3            3           3                                    |                           \                      x    / |       2           2                                  ||
                          \                                                            \                            x            x           x                                     /                                                         \      x           x                                   //

$$- 10 \left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right)^{7} \cdot \left(2 \left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right)^{2} \cdot \left(250 \left(\cot^{2}{\left(5 x \right)} + 1\right) \cot^{2}{\left(5 x \right)} - \frac{7 \log{\left(x \right)}^{6}}{x^{3}} + 125 \left(\cot^{2}{\left(5 x \right)} + 1\right)^{2} + \frac{63 \log{\left(x \right)}^{5}}{x^{3}} - \frac{105 \log{\left(x \right)}^{4}}{x^{3}}\right) + 27 \left(\log{\left(x \right)}^{7} + \cot{\left(5 x \right)}\right) \left(- \frac{7 \log{\left(x \right)}^{6}}{x^{2}} + \frac{42 \log{\left(x \right)}^{5}}{x^{2}} + 50 \left(\cot^{2}{\left(5 x \right)} + 1\right) \cot{\left(5 x \right)}\right) \left(- \frac{7 \log{\left(x \right)}^{6}}{x} + 5 \cot^{2}{\left(5 x \right)} + 5\right) + 72 \left(- \frac{7 \log{\left(x \right)}^{6}}{x} + 5 \cot^{2}{\left(5 x \right)} + 5\right)^{3}\right)$$

Simplify

The graph

Other calculators

How to use it?

Identical expressions

Similar expressions

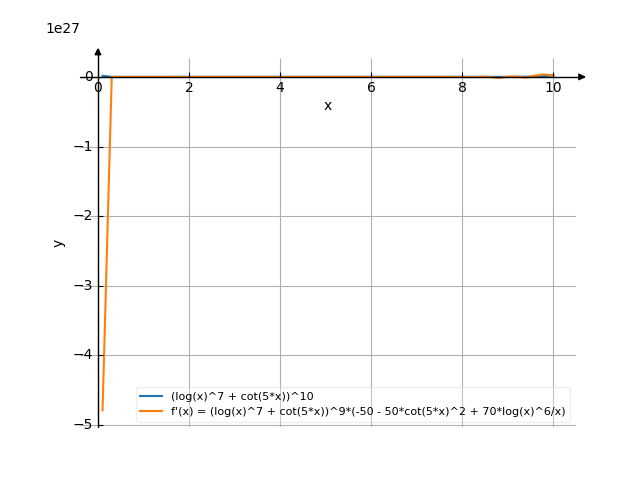
Derivative of (ln^7x+ctg5x)^10

The graph:

Piecewise:

The solution

Method #1

Method #2