Derivative of ln(arccos*(1/sqrtx))
The solution
You have entered
[src]
/ / 1 \\ log|acos|1*-----|| | | ___|| \ \ \/ x //
$$\log{\left(\operatorname{acos}{\left(1 \cdot \frac{1}{\sqrt{x}} \right)} \right)}$$
d / / / 1 \\\ --|log|acos|1*-----||| dx| | | ___||| \ \ \ \/ x ///
$$\frac{d}{d x} \log{\left(\operatorname{acos}{\left(1 \cdot \frac{1}{\sqrt{x}} \right)} \right)}$$
The first derivative
[src]
1
--------------------------------
_______
3/2 / 1 / 1 \
2*x * / 1 - - *acos|1*-----|
\/ x | ___|
\ \/ x /
$$\frac{1}{2 x^{\frac{3}{2}} \sqrt{1 - \frac{1}{x}} \operatorname{acos}{\left(1 \cdot \frac{1}{\sqrt{x}} \right)}}$$
The second derivative
[src]
/ 1 3 1 \
-|--------------- + ---------------- + ----------------------|
| 3/2 _______ 3 / 1\ / 1 \|
| 7/2 / 1\ 5/2 / 1 x *|1 - -|*acos|-----||
|x *|1 - -| x * / 1 - - \ x/ | ___||
\ \ x/ \/ x \\/ x //
---------------------------------------------------------------
/ 1 \
4*acos|-----|
| ___|
\\/ x /
$$- \frac{\frac{1}{x^{3} \cdot \left(1 - \frac{1}{x}\right) \operatorname{acos}{\left(\frac{1}{\sqrt{x}} \right)}} + \frac{3}{x^{\frac{5}{2}} \sqrt{1 - \frac{1}{x}}} + \frac{1}{x^{\frac{7}{2}} \left(1 - \frac{1}{x}\right)^{\frac{3}{2}}}}{4 \operatorname{acos}{\left(\frac{1}{\sqrt{x}} \right)}}$$
The third derivative
[src]
3 10 15 2 3 9
---------------- + --------------- + ---------------- + ---------------------------- + ----------------------- + ----------------------
5/2 3/2 _______ 3/2 2 4 / 1\ / 1 \
11/2 / 1\ 9/2 / 1\ 7/2 / 1 9/2 / 1\ 2/ 1 \ 5 / 1\ / 1 \ x *|1 - -|*acos|-----|
x *|1 - -| x *|1 - -| x * / 1 - - x *|1 - -| *acos |-----| x *|1 - -| *acos|-----| \ x/ | ___|
\ x/ \ x/ \/ x \ x/ | ___| \ x/ | ___| \\/ x /
\\/ x / \\/ x /
---------------------------------------------------------------------------------------------------------------------------------------
/ 1 \
8*acos|-----|
| ___|
\\/ x /
$$\frac{\frac{9}{x^{4} \cdot \left(1 - \frac{1}{x}\right) \operatorname{acos}{\left(\frac{1}{\sqrt{x}} \right)}} + \frac{3}{x^{5} \left(1 - \frac{1}{x}\right)^{2} \operatorname{acos}{\left(\frac{1}{\sqrt{x}} \right)}} + \frac{15}{x^{\frac{7}{2}} \sqrt{1 - \frac{1}{x}}} + \frac{10}{x^{\frac{9}{2}} \left(1 - \frac{1}{x}\right)^{\frac{3}{2}}} + \frac{2}{x^{\frac{9}{2}} \left(1 - \frac{1}{x}\right)^{\frac{3}{2}} \operatorname{acos}^{2}{\left(\frac{1}{\sqrt{x}} \right)}} + \frac{3}{x^{\frac{11}{2}} \left(1 - \frac{1}{x}\right)^{\frac{5}{2}}}}{8 \operatorname{acos}{\left(\frac{1}{\sqrt{x}} \right)}}$$
The graph
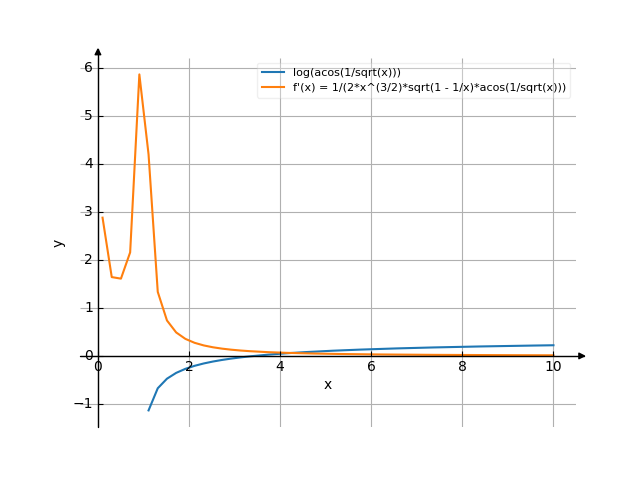

![Find the derivative of y' = f'(x) = ln(arccos*(1/sqrtx)) (ln(arc co sinus of e of multiply by (1 divide by square root of x))) - functions. Find the derivative of the function at the point. [THERE'S THE ANSWER!] ln(arccos*(1/sqrtx))](/media/krcore-image-pods/176/hash/derivative/5/ba/bfb9b43b774d389d2ba29e74168df.png)
 Derivative of -4*y-y^2
Derivative of -4*y-y^2
 Derivative of 4-2x
Derivative of 4-2x
 Derivative of 1/(2x)
Derivative of 1/(2x)
 Derivative of e^sin(x)^(2)
Derivative of e^sin(x)^(2)