Derivative of arctg(x^2-4x)
The solution
You have entered
[src]
/ 2 \ atan\x - 4*x/
$$\operatorname{atan}{\left(x^{2} - 4 x \right)}$$
d / / 2 \\ --\atan\x - 4*x// dx
$$\frac{d}{d x} \operatorname{atan}{\left(x^{2} - 4 x \right)}$$
The first derivative
[src]
-4 + 2*x
---------------
2
/ 2 \
1 + \x - 4*x/
$$\frac{2 x - 4}{\left(x^{2} - 4 x\right)^{2} + 1}$$
The second derivative
[src]
/ 2 \
| 4*x*(-2 + x) *(-4 + x)|
2*|1 - ----------------------|
| 2 2 |
\ 1 + x *(-4 + x) /
------------------------------
2 2
1 + x *(-4 + x)
$$\frac{2 \left(- \frac{4 x \left(x - 4\right) \left(x - 2\right)^{2}}{x^{2} \left(x - 4\right)^{2} + 1} + 1\right)}{x^{2} \left(x - 4\right)^{2} + 1}$$
The third derivative
[src]
/ 2 2 2\
| 2 8*x *(-4 + x) *(-2 + x) |
8*(-2 + x)*|- 2*(-2 + x) - 3*x*(-4 + x) + ------------------------|
| 2 2 |
\ 1 + x *(-4 + x) /
--------------------------------------------------------------------
2
/ 2 2\
\1 + x *(-4 + x) /
$$\frac{8 \left(x - 2\right) \left(\frac{8 x^{2} \left(x - 4\right)^{2} \left(x - 2\right)^{2}}{x^{2} \left(x - 4\right)^{2} + 1} - 3 x \left(x - 4\right) - 2 \left(x - 2\right)^{2}\right)}{\left(x^{2} \left(x - 4\right)^{2} + 1\right)^{2}}$$
The graph
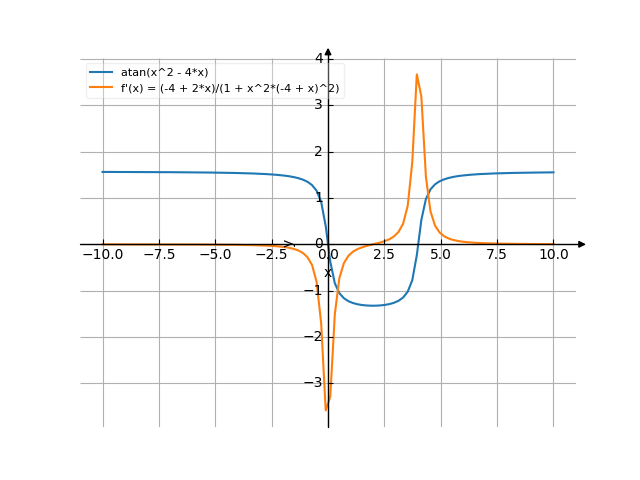

![Find the derivative of y' = f'(x) = arctg(x²-4x) (arctg(x squared minus 4x)) - functions. Find the derivative of the function at the point. [THERE'S THE ANSWER!] arctg(x^2-4x)](/media/krcore-image-pods/176/hash/derivative/8/55/0dfe8a37b2a16bf3a6baf1e3145a6.png)
 Derivative of x*ctgx
Derivative of x*ctgx
 Derivative of x^6/6
Derivative of x^6/6
 Derivative of (x-3)^4
Derivative of (x-3)^4
 Derivative of x*e^(3*x)
Derivative of x*e^(3*x)