Mister Exam

Other calculators

arctg(x)^(lnx)
The derivative of the function/ arctg(x)^(lnx)

Derivative of arctg(x)^(lnx)

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
    log(x)   
atan      (x)
atan⁡log⁡(x)(x)\operatorname{atan}^{\log{\left(x \right)}}{\left(x \right)} 
d /    log(x)   \
--\atan      (x)/
dx
ddxatan⁡log⁡(x)(x)\frac{d}{d x} \operatorname{atan}^{\log{\left(x \right)}}{\left(x \right)}
Transform
Detail solution

  1. Don't know the steps in finding this derivative.

    But the derivative is

    (log⁡(log⁡(x))+1)log⁡(x)log⁡(x)\left(\log{\left(\log{\left(x \right)} \right)} + 1\right) \log{\left(x \right)}^{\log{\left(x \right)}}

The answer is:

(log⁡(log⁡(x))+1)log⁡(x)log⁡(x)\left(\log{\left(\log{\left(x \right)} \right)} + 1\right) \log{\left(x \right)}^{\log{\left(x \right)}}

The graph
02468-8-6-4-2-1010-1000010000
Plot the graph f(x)
Plot the graph f'(x)
The first derivative [src] 
    log(x)    /log(atan(x))        log(x)     \
atan      (x)*|------------ + ----------------|
              |     x         /     2\        |
              \               \1 + x /*atan(x)/
(log⁡(x)(x2+1)atan⁡(x)+log⁡(atan⁡(x))x)atan⁡log⁡(x)(x)\left(\frac{\log{\left(x \right)}}{\left(x^{2} + 1\right) \operatorname{atan}{\left(x \right)}} + \frac{\log{\left(\operatorname{atan}{\left(x \right)} \right)}}{x}\right) \operatorname{atan}^{\log{\left(x \right)}}{\left(x \right)}
Simplify
The second derivative [src] 
              /                                 2                                                                             \
    log(x)    |/log(atan(x))        log(x)     \    log(atan(x))         log(x)                 2                2*x*log(x)   |
atan      (x)*||------------ + ----------------|  - ------------ - ------------------ + ------------------ - -----------------|
              ||     x         /     2\        |          2                2              /     2\                   2        |
              |\               \1 + x /*atan(x)/         x         /     2\      2      x*\1 + x /*atan(x)   /     2\         |
              \                                                    \1 + x / *atan (x)                        \1 + x / *atan(x)/
(−2xlog⁡(x)(x2+1)2atan⁡(x)+(log⁡(x)(x2+1)atan⁡(x)+log⁡(atan⁡(x))x)2−log⁡(x)(x2+1)2atan⁡2(x)+2x(x2+1)atan⁡(x)−log⁡(atan⁡(x))x2)atan⁡log⁡(x)(x)\left(- \frac{2 x \log{\left(x \right)}}{\left(x^{2} + 1\right)^{2} \operatorname{atan}{\left(x \right)}} + \left(\frac{\log{\left(x \right)}}{\left(x^{2} + 1\right) \operatorname{atan}{\left(x \right)}} + \frac{\log{\left(\operatorname{atan}{\left(x \right)} \right)}}{x}\right)^{2} - \frac{\log{\left(x \right)}}{\left(x^{2} + 1\right)^{2} \operatorname{atan}^{2}{\left(x \right)}} + \frac{2}{x \left(x^{2} + 1\right) \operatorname{atan}{\left(x \right)}} - \frac{\log{\left(\operatorname{atan}{\left(x \right)} \right)}}{x^{2}}\right) \operatorname{atan}^{\log{\left(x \right)}}{\left(x \right)}
Simplify
The third derivative [src] 
              /                                 3                                                                                                                                                                                                                                                                            2          \
    log(x)    |/log(atan(x))        log(x)     \            6             /log(atan(x))        log(x)     \ /log(atan(x))         log(x)                 2                2*x*log(x)   \   2*log(atan(x))            3                      3                 2*log(x)            2*log(x)            6*x*log(x)          8*x *log(x)   |
atan      (x)*||------------ + ----------------|  - ----------------- - 3*|------------ + ----------------|*|------------ + ------------------ - ------------------ + -----------------| + -------------- - -------------------- - ------------------- - ----------------- + ------------------ + ------------------ + -----------------|
              ||     x         /     2\        |            2             |     x         /     2\        | |      2                2              /     2\                   2        |          3                   2             2 /     2\                   2                   3                    3                    3        |
              |\               \1 + x /*atan(x)/    /     2\              \               \1 + x /*atan(x)/ |     x         /     2\      2      x*\1 + x /*atan(x)   /     2\         |         x            /     2\      2      x *\1 + x /*atan(x)   /     2\            /     2\      3      /     2\      2      /     2\         |
              \                                     \1 + x / *atan(x)                                       \               \1 + x / *atan (x)                        \1 + x / *atan(x)/                    x*\1 + x / *atan (x)                         \1 + x / *atan(x)   \1 + x / *atan (x)   \1 + x / *atan (x)   \1 + x / *atan(x)/
(8x2log⁡(x)(x2+1)3atan⁡(x)+6xlog⁡(x)(x2+1)3atan⁡2(x)+(log⁡(x)(x2+1)atan⁡(x)+log⁡(atan⁡(x))x)3−3(log⁡(x)(x2+1)atan⁡(x)+log⁡(atan⁡(x))x)(2xlog⁡(x)(x2+1)2atan⁡(x)+log⁡(x)(x2+1)2atan⁡2(x)−2x(x2+1)atan⁡(x)+log⁡(atan⁡(x))x2)−2log⁡(x)(x2+1)2atan⁡(x)−6(x2+1)2atan⁡(x)+2log⁡(x)(x2+1)3atan⁡3(x)−3x(x2+1)2atan⁡2(x)−3x2(x2+1)atan⁡(x)+2log⁡(atan⁡(x))x3)atan⁡log⁡(x)(x)\left(\frac{8 x^{2} \log{\left(x \right)}}{\left(x^{2} + 1\right)^{3} \operatorname{atan}{\left(x \right)}} + \frac{6 x \log{\left(x \right)}}{\left(x^{2} + 1\right)^{3} \operatorname{atan}^{2}{\left(x \right)}} + \left(\frac{\log{\left(x \right)}}{\left(x^{2} + 1\right) \operatorname{atan}{\left(x \right)}} + \frac{\log{\left(\operatorname{atan}{\left(x \right)} \right)}}{x}\right)^{3} - 3 \left(\frac{\log{\left(x \right)}}{\left(x^{2} + 1\right) \operatorname{atan}{\left(x \right)}} + \frac{\log{\left(\operatorname{atan}{\left(x \right)} \right)}}{x}\right) \left(\frac{2 x \log{\left(x \right)}}{\left(x^{2} + 1\right)^{2} \operatorname{atan}{\left(x \right)}} + \frac{\log{\left(x \right)}}{\left(x^{2} + 1\right)^{2} \operatorname{atan}^{2}{\left(x \right)}} - \frac{2}{x \left(x^{2} + 1\right) \operatorname{atan}{\left(x \right)}} + \frac{\log{\left(\operatorname{atan}{\left(x \right)} \right)}}{x^{2}}\right) - \frac{2 \log{\left(x \right)}}{\left(x^{2} + 1\right)^{2} \operatorname{atan}{\left(x \right)}} - \frac{6}{\left(x^{2} + 1\right)^{2} \operatorname{atan}{\left(x \right)}} + \frac{2 \log{\left(x \right)}}{\left(x^{2} + 1\right)^{3} \operatorname{atan}^{3}{\left(x \right)}} - \frac{3}{x \left(x^{2} + 1\right)^{2} \operatorname{atan}^{2}{\left(x \right)}} - \frac{3}{x^{2} \left(x^{2} + 1\right) \operatorname{atan}{\left(x \right)}} + \frac{2 \log{\left(\operatorname{atan}{\left(x \right)} \right)}}{x^{3}}\right) \operatorname{atan}^{\log{\left(x \right)}}{\left(x \right)}
Simplify
The graph
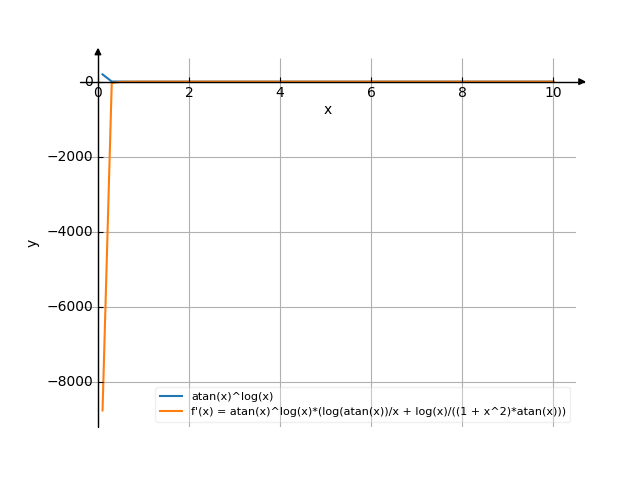
Derivative of arctg(x)^(lnx)
    © Mister Exam – Calculator