Mister Exam

Lang:

Other calculators

How to use it?
Derivative of:
Derivative of (4x^3-3x^2)/(2x-1)^2
Derivative of 6sin(x)
Derivative of 3sinxcosx
Derivative of 8sin2x
Identical expressions
(4x^ three -3x^ two)/(two x- one)^2
(4x cubed minus 3x squared ) divide by (2x minus 1) squared
(4x to the power of three minus 3x to the power of two) divide by (two x minus one) squared
(4x3-3x2)/(2x-1)2
4x3-3x2/2x-12
(4x³-3x²)/(2x-1)²
(4x to the power of 3-3x to the power of 2)/(2x-1) to the power of 2
4x^3-3x^2/2x-1^2
(4x^3-3x^2) divide by (2x-1)^2
Similar expressions
(4x^3-3x^2)/(2x+1)^2
(4x^3+3x^2)/(2x-1)^2

The derivative of the function/ (4x^3-3x^2)/(2x-1)^2

Derivative of (4x^3-3x^2)/(2x-1)^2

The solution

You have entered [src]

   3      2
4*x  - 3*x 
-----------
          2
 (2*x - 1)

$$\frac{4 x^{3} - 3 x^{2}}{\left(2 x - 1\right)^{2}}$$

  /   3      2\
d |4*x  - 3*x |
--|-----------|
dx|          2|
  \ (2*x - 1) /

$$\frac{d}{d x} \frac{4 x^{3} - 3 x^{2}}{\left(2 x - 1\right)^{2}}$$

Transform

Detail solution

Apply the quotient rule, which is:

$\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}$

$f{\left(x \right)} = 4 x^{3} - 3 x^{2}$ and $g{\left(x \right)} = \left(2 x - 1\right)^{2}$ .

To find $\frac{d}{d x} f{\left(x \right)}$ :
1. Differentiate $4 x^{3} - 3 x^{2}$ term by term:
  1. The derivative of a constant times a function is the constant times the derivative of the function.
    1. Apply the power rule: $x^{2}$ goes to $2 x$
    So, the result is: $- 6 x$
  2. The derivative of a constant times a function is the constant times the derivative of the function.
    1. Apply the power rule: $x^{3}$ goes to $3 x^{2}$
    So, the result is: $12 x^{2}$
  The result is: $12 x^{2} - 6 x$
To find $\frac{d}{d x} g{\left(x \right)}$ :
1. Let $u = 2 x - 1$ .
2. Apply the power rule: $u^{2}$ goes to $2 u$
3. Then, apply the chain rule. Multiply by $\frac{d}{d x} \left(2 x - 1\right)$ :
  1. Differentiate $2 x - 1$ term by term:
    1. The derivative of the constant $-1$ is zero.
    2. The derivative of a constant times a function is the constant times the derivative of the function.
      1. Apply the power rule: $x$ goes to $1$
      So, the result is: $2$
    The result is: $2$
  The result of the chain rule is:
  
  $8 x - 4$
Now plug in to the quotient rule:

$\frac{\left(2 x - 1\right)^{2} \cdot \left(12 x^{2} - 6 x\right) - \left(8 x - 4\right) \left(4 x^{3} - 3 x^{2}\right)}{\left(2 x - 1\right)^{4}}$
Now simplify:

$\frac{2 x \left(- 2 x \left(4 x - 3\right) + 3 \left(2 x - 1\right)^{2}\right)}{\left(2 x - 1\right)^{3}}$

The answer is:

$\frac{2 x \left(- 2 x \left(4 x - 3\right) + 3 \left(2 x - 1\right)^{2}\right)}{\left(2 x - 1\right)^{3}}$

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

           2             /   3      2\
-6*x + 12*x    (4 - 8*x)*\4*x  - 3*x /
------------ + -----------------------
          2                    4      
 (2*x - 1)            (2*x - 1)

$$\frac{12 x^{2} - 6 x}{\left(2 x - 1\right)^{2}} + \frac{\left(- 8 x + 4\right) \left(4 x^{3} - 3 x^{2}\right)}{\left(2 x - 1\right)^{4}}$$

Simplify

The second derivative [src]

  /              2           \
  |           4*x *(-3 + 4*x)|
6*|-1 - 4*x + ---------------|
  |                       2  |
  \             (-1 + 2*x)   /
------------------------------
                   2          
         (-1 + 2*x)

$$\frac{6 \cdot \left(\frac{4 x^{2} \cdot \left(4 x - 3\right)}{\left(2 x - 1\right)^{2}} - 4 x - 1\right)}{\left(2 x - 1\right)^{2}}$$

Simplify

The third derivative [src]

   /                                 2           \
   |    3*(-1 + 4*x)     18*x     8*x *(-3 + 4*x)|
24*|1 - ------------ + -------- - ---------------|
   |      -1 + 2*x     -1 + 2*x               3  |
   \                                (-1 + 2*x)   /
--------------------------------------------------
                             2                    
                   (-1 + 2*x)

$$\frac{24 \left(- \frac{8 x^{2} \cdot \left(4 x - 3\right)}{\left(2 x - 1\right)^{3}} + \frac{18 x}{2 x - 1} + 1 - \frac{3 \cdot \left(4 x - 1\right)}{2 x - 1}\right)}{\left(2 x - 1\right)^{2}}$$

Simplify

The graph

Other calculators

How to use it?

Identical expressions

Similar expressions

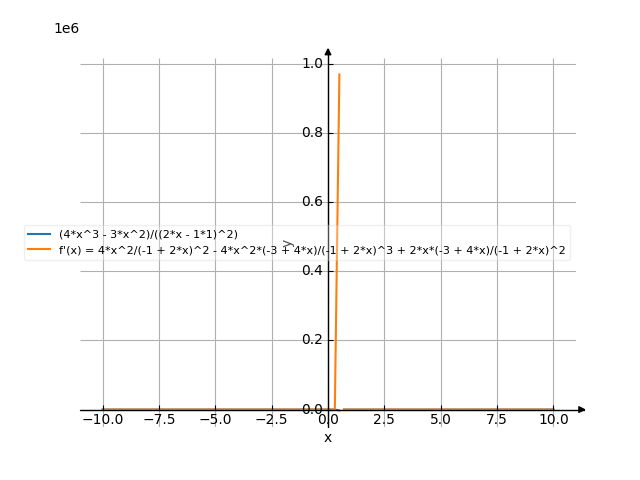
Derivative of (4x^3-3x^2)/(2x-1)^2

The graph:

Piecewise:

The solution