Other limits x→0, -oo, +oo, 1
x→−∞limacos(x)=−∞ix→∞limacos(x)=∞iMore at x→oox→0−limacos(x)=2πMore at x→0 from the leftx→0+limacos(x)=2πMore at x→0 from the rightx→1−limacos(x)=0More at x→1 from the leftx→1+limacos(x)=0More at x→1 from the right


![Limit of the function lim y = f(x) = acos(x) (arc co sinus of e of ine of (x)) at point x -> -oo and infinity - find and calculate with the detailed solution [THERE'S THE ANSWER!] acos(x)](/media/krcore-image-pods/176/2/e2/ca96856e5e3e121faa7db6e9a80f3.png)
 Limit of (e^x-e^2)/(-2+x)
Limit of (e^x-e^2)/(-2+x)
 Limit of (-asin(x)+2*x)/(2*x+atan(x))
Limit of (-asin(x)+2*x)/(2*x+atan(x))
 Limit of (16+x^2+10*x)/(-6+x^2-x)
Limit of (16+x^2+10*x)/(-6+x^2-x)
 Limit of n*(2+n)/(1+n)^2
Limit of n*(2+n)/(1+n)^2
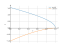 acos(x)
acos(x)
 acos(x)
acos(x)