Mister Exam
Other calculators
- Improper integral
- Double Integral
- Triple Integral
- Curvilinear integral
- Derivative Step by Step
- Differential equations Step by Step
- Limits Step by Step
-
How to use it?
- Integral of d{x}:
-
Integral of 1/(2+x^2)
- Integral of sin(w*t)^2
- Integral of sin(log(x))^2/x
- Integral of sin^n(x)
-
Identical expressions
- x^2sin^3x
- x squared sinus of cubed x
- x2sin3x
- x²sin³x
- x to the power of 2sin to the power of 3x
- x^2sin^3xdx
Integral of x^2sin^3x dx
The solution
You have entered
[src]
1 / | | 2 3 | x *sin (x) dx | / 0
$$\int\limits_{0}^{1} x^{2} \sin^{3}{\left(x \right)}\, dx$$
Integral(x^2*sin(x)^3, (x, 0, 1))
The answer (Indefinite)
[src]
/ | 3 2 3 3 2 2 | 2 3 40*cos (x) 2*x *cos (x) 14*x*sin (x) 14*sin (x)*cos(x) 2 2 4*x*cos (x)*sin(x) | x *sin (x) dx = C + ---------- - ------------ + ------------ + ----------------- - x *sin (x)*cos(x) + ------------------ | 27 3 9 9 3 /
$$\int x^{2} \sin^{3}{\left(x \right)}\, dx = C - x^{2} \sin^{2}{\left(x \right)} \cos{\left(x \right)} - \frac{2 x^{2} \cos^{3}{\left(x \right)}}{3} + \frac{14 x \sin^{3}{\left(x \right)}}{9} + \frac{4 x \sin{\left(x \right)} \cos^{2}{\left(x \right)}}{3} + \frac{14 \sin^{2}{\left(x \right)} \cos{\left(x \right)}}{9} + \frac{40 \cos^{3}{\left(x \right)}}{27}$$
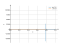
The graph
The answer
[src]
3 3 2 2 40 14*sin (1) 22*cos (1) 4*cos (1)*sin(1) 5*sin (1)*cos(1) - -- + ---------- + ---------- + ---------------- + ---------------- 27 9 27 3 9
$$- \frac{40}{27} + \frac{22 \cos^{3}{\left(1 \right)}}{27} + \frac{5 \sin^{2}{\left(1 \right)} \cos{\left(1 \right)}}{9} + \frac{4 \sin{\left(1 \right)} \cos^{2}{\left(1 \right)}}{3} + \frac{14 \sin^{3}{\left(1 \right)}}{9}$$
=
=
3 3 2 2 40 14*sin (1) 22*cos (1) 4*cos (1)*sin(1) 5*sin (1)*cos(1) - -- + ---------- + ---------- + ---------------- + ---------------- 27 9 27 3 9
$$- \frac{40}{27} + \frac{22 \cos^{3}{\left(1 \right)}}{27} + \frac{5 \sin^{2}{\left(1 \right)} \cos{\left(1 \right)}}{9} + \frac{4 \sin{\left(1 \right)} \cos^{2}{\left(1 \right)}}{3} + \frac{14 \sin^{3}{\left(1 \right)}}{9}$$
-40/27 + 14*sin(1)^3/9 + 22*cos(1)^3/27 + 4*cos(1)^2*sin(1)/3 + 5*sin(1)^2*cos(1)/9
The graph
Use the examples entering the upper and lower limits of integration.