Mister Exam
Other calculators
- Improper integral
- Double Integral
- Triple Integral
- Curvilinear integral
- Derivative Step by Step
- Differential equations Step by Step
- Limits Step by Step
-
How to use it?
- Integral of d{x}:
-
Integral of x^e
-
Integral of √(x+4)
-
Integral of sqrt(1+x^4)
-
Integral of sin(2x)cos(2x)
-
Identical expressions
- sqrt(one +x^ four)
- square root of (1 plus x to the power of 4)
- square root of (one plus x to the power of four)
- √(1+x^4)
- sqrt(1+x4)
- sqrt1+x4
- sqrt(1+x⁴)
- sqrt1+x^4
- sqrt(1+x^4)dx
-
Similar expressions
- sqrt(1-x^4)
Integral of sqrt(1+x^4) dx
The solution
You have entered
[src]
1 / | | ________ | / 4 | \/ 1 + x dx | / 0
$$\int\limits_{0}^{1} \sqrt{x^{4} + 1}\, dx$$
Integral(sqrt(1 + x^4), (x, 0, 1))
The answer (Indefinite)
[src]
/ _ | |_ /-1/2, 1/4 | 4 pi*I\ | ________ x*Gamma(1/4)* | | | x *e | | / 4 2 1 \ 5/4 | / | \/ 1 + x dx = C + ---------------------------------------- | 4*Gamma(5/4) /
$$\int \sqrt{x^{4} + 1}\, dx = C + \frac{x \Gamma\left(\frac{1}{4}\right) {{}_{2}F_{1}\left(\begin{matrix} - \frac{1}{2}, \frac{1}{4} \\ \frac{5}{4} \end{matrix}\middle| {x^{4} e^{i \pi}} \right)}}{4 \Gamma\left(\frac{5}{4}\right)}$$
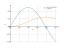
The graph
The answer
[src]
_
|_ /-1/2, 1/4 | \
Gamma(1/4)* | | | -1|
2 1 \ 5/4 | /
--------------------------------
4*Gamma(5/4)
$$\frac{\Gamma\left(\frac{1}{4}\right) {{}_{2}F_{1}\left(\begin{matrix} - \frac{1}{2}, \frac{1}{4} \\ \frac{5}{4} \end{matrix}\middle| {-1} \right)}}{4 \Gamma\left(\frac{5}{4}\right)}$$
=
=
_
|_ /-1/2, 1/4 | \
Gamma(1/4)* | | | -1|
2 1 \ 5/4 | /
--------------------------------
4*Gamma(5/4)
$$\frac{\Gamma\left(\frac{1}{4}\right) {{}_{2}F_{1}\left(\begin{matrix} - \frac{1}{2}, \frac{1}{4} \\ \frac{5}{4} \end{matrix}\middle| {-1} \right)}}{4 \Gamma\left(\frac{5}{4}\right)}$$
gamma(1/4)*hyper((-1/2, 1/4), (5/4,), -1)/(4*gamma(5/4))
The graph
Use the examples entering the upper and lower limits of integration.