Mister Exam
Other calculators
- Improper integral
- Double Integral
- Triple Integral
- Curvilinear integral
- Derivative Step by Step
- Differential equations Step by Step
- Limits Step by Step
-
How to use it?
- Integral of d{x}:
-
Integral of e^(2*x+1)
-
Integral of e^x²
-
Integral of (-x)/(1+x^2)
-
Integral of sqrt(x^2+4)/x^2
-
Identical expressions
- (-x)/(one +x^ two)
- ( minus x) divide by (1 plus x squared )
- ( minus x) divide by (one plus x to the power of two)
- (-x)/(1+x2)
- -x/1+x2
- (-x)/(1+x²)
- (-x)/(1+x to the power of 2)
- -x/1+x^2
- (-x) divide by (1+x^2)
- (-x)/(1+x^2)dx
-
Similar expressions
- (x)/(1+x^2)
- (-x)/(1-x^2)
Integral of (-x)/(1+x^2) dx
The solution
You have entered
[src]
1 / | | -x | ------ dx | 2 | 1 + x | / 0
$$\int\limits_{0}^{1} \frac{\left(-1\right) x}{x^{2} + 1}\, dx$$
Integral((-x)/(1 + x^2), (x, 0, 1))
Detail solution
We have the integral:
/ | | -x | ------ dx | 2 | 1 + x | /
Rewrite the integrand
/ 2*x \
|------------| /0\
| 2 | |-|
-x \x + 0*x + 1/ \1/
------ = - -------------- + ---------
2 2 2
1 + x (-x) + 1or
/ | | -x | ------ dx | 2 = | 1 + x | /
/
|
| 2*x
- | ------------ dx
| 2
| x + 0*x + 1
|
/
--------------------
2 In the integral
/
|
| 2*x
- | ------------ dx
| 2
| x + 0*x + 1
|
/
--------------------
2 do replacement
2 u = x
then
the integral =
/
|
| 1
- | ----- du
| 1 + u
|
/ -log(1 + u)
------------- = ------------
2 2 do backward replacement
/
|
| 2*x
- | ------------ dx
| 2
| x + 0*x + 1
| / 2\
/ -log\1 + x /
-------------------- = -------------
2 2 In the integral
0
do replacement
v = -x
then
the integral =
True
do backward replacement
True
Solution is:
/ 2\
log\1 + x /
C - -----------
2
The answer (Indefinite)
[src]
/ | / 2\ | -x log\1 + x / | ------ dx = C - ----------- | 2 2 | 1 + x | /
$$\int \frac{\left(-1\right) x}{x^{2} + 1}\, dx = C - \frac{\log{\left(x^{2} + 1 \right)}}{2}$$
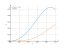
The graph
The answer
[src]
-log(2) -------- 2
$$- \frac{\log{\left(2 \right)}}{2}$$
=
=
-log(2) -------- 2
$$- \frac{\log{\left(2 \right)}}{2}$$
-log(2)/2
The graph
Use the examples entering the upper and lower limits of integration.