Mister Exam

Other calculators

cos(0,02x^3)
Solving integrals/ cos(0,02x^3)

Integral of cos(0,02x^3) dx

Limits of integration:

from to
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
 31/5          
   /           
  |            
  |     / 3\   
  |     |x |   
  |  cos|--| dx
  |     \50/   
  |            
 /             
23/5
∫235315cos⁡(x350) dx\int\limits_{\frac{23}{5}}^{\frac{31}{5}} \cos{\left(\frac{x^{3}}{50} \right)}\, dx 
Integral(cos(x^3/50), (x, 23/5, 31/5))
The answer (Indefinite) [src] 
                                                        
  /                                _  /         |    6 \
 |                                |_  |  1/6    |  -x  |
 |    / 3\          x*Gamma(1/6)* |   |         | -----|
 |    |x |                       1  2 \1/2, 7/6 | 10000/
 | cos|--| dx = C + ------------------------------------
 |    \50/                      6*Gamma(7/6)            
 |                                                      
/
5013 i Γ(13,i x350)−5013 i Γ(13,−i x350)12{{50^{{{1}\over{3}}}\,i\,\Gamma\left({{1}\over{3}} , {{i\,x^3 }\over{50}}\right)-50^{{{1}\over{3}}}\,i\,\Gamma\left({{1}\over{3}} , -{{i\,x^3}\over{50}}\right)}\over{12}}
Simplify
The graph
6.24.64.85.05.25.45.65.86.05-5
Plot the graph f(x)
The answer [src] 
                  _                                             _                          
                 |_  /  1/6    | -148035889 \                  |_  /  1/6    | -887503681 \
  23*Gamma(1/6)* |   |         | -----------|   31*Gamma(1/6)* |   |         | -----------|
                1  2 \1/2, 7/6 |  156250000 /                 1  2 \1/2, 7/6 |  156250000 /
- ------------------------------------------- + -------------------------------------------
                 30*Gamma(7/6)                                 30*Gamma(7/6)
5013 i Γ(13,29791 i6250)12−5013 i Γ(13,12167 i6250)12+5013 i Γ(13,−12167 i6250)12−5013 i Γ(13,−29791 i6250)12{{50^{{{1}\over{3}}}\,i\,\Gamma\left({{1}\over{3}} , {{29791\,i }\over{6250}}\right)}\over{12}}-{{50^{{{1}\over{3}}}\,i\,\Gamma \left({{1}\over{3}} , {{12167\,i}\over{6250}}\right)}\over{12}}+{{50 ^{{{1}\over{3}}}\,i\,\Gamma\left({{1}\over{3}} , -{{12167\,i}\over{ 6250}}\right)}\over{12}}-{{50^{{{1}\over{3}}}\,i\,\Gamma\left({{1 }\over{3}} , -{{29791\,i}\over{6250}}\right)}\over{12}} 
=
= 
                  _                                             _                          
                 |_  /  1/6    | -148035889 \                  |_  /  1/6    | -887503681 \
  23*Gamma(1/6)* |   |         | -----------|   31*Gamma(1/6)* |   |         | -----------|
                1  2 \1/2, 7/6 |  156250000 /                 1  2 \1/2, 7/6 |  156250000 /
- ------------------------------------------- + -------------------------------------------
                 30*Gamma(7/6)                                 30*Gamma(7/6)
31Γ(16)1F2(1612,76|−887503681156250000)30Γ(76)−23Γ(16)1F2(1612,76|−148035889156250000)30Γ(76)\frac{31 \Gamma\left(\frac{1}{6}\right) {{}_{1}F_{2}\left(\begin{matrix} \frac{1}{6} \\ \frac{1}{2}, \frac{7}{6} \end{matrix}\middle| {- \frac{887503681}{156250000}} \right)}}{30 \Gamma\left(\frac{7}{6}\right)} - \frac{23 \Gamma\left(\frac{1}{6}\right) {{}_{1}F_{2}\left(\begin{matrix} \frac{1}{6} \\ \frac{1}{2}, \frac{7}{6} \end{matrix}\middle| {- \frac{148035889}{156250000}} \right)}}{30 \Gamma\left(\frac{7}{6}\right)}
Simplify
Numerical answer [src] 
-1.11978994372684
-1.11978994372684
The graph
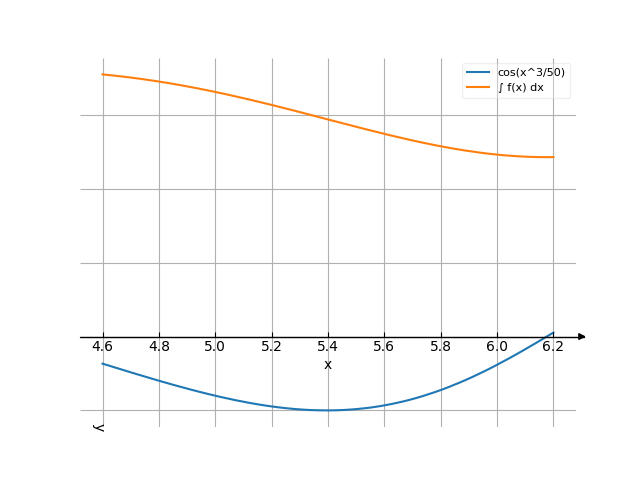
Integral of cos(0,02x^3) dx

    Use the examples entering the upper and lower limits of integration.

    © Mister Exam – Calculator