Intégrale 2x³ dx
Solution
Detail solution
-
The integral of a constant times a function is the constant times the integral of the function:
-
The integral of is when :
So, the result is:
-
-
Add the constant of integration:
The answer is:
The graph
Graphique

Ces exemples peuvent également être utilisés lors de la saisie des bornes supérieure et inférieure d’intégration.

![Trouver l’intégrale de y = f(x) = 2x³ dx (2x³) - avec solution détaillée [IL Y A UNE RÉPONSE !] 2x³](/media/krcore-image-pods/176/hash/indefinite/3/83/921c4b69be8059d55edac55a9ab67.png)
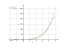 Intégrale 2x³
Intégrale 2x³
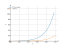 Intégrale e^(5x)*sin(x)
Intégrale e^(5x)*sin(x)
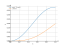 Intégrale sin^2t*cost
Intégrale sin^2t*cost
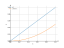 Intégrale xdt
Intégrale xdt
 2x³
2x³