x⁴>256 inequation
The solution
Detail solution
Given the inequality:
$$x^{4} > 256$$
To solve this inequality, we must first solve the corresponding equation:
$$x^{4} = 256$$
Solve:
Given the equation
$$x^{4} = 256$$
Because equation degree is equal to = 4 - contains the even number 4 in the numerator, then
the equation has two real roots.
Get the root 4-th degree of the equation sides:
We get:
$$\sqrt[4]{x^{4}} = \sqrt[4]{256}$$
$$\sqrt[4]{x^{4}} = \left(-1\right) \sqrt[4]{256}$$
or
$$x = 4$$
$$x = -4$$
We get the answer: x = 4
We get the answer: x = -4
or
$$x_{1} = -4$$
$$x_{2} = 4$$
All other 2 root(s) is the complex numbers.
do replacement:
$$z = x$$
then the equation will be the:
$$z^{4} = 256$$
Any complex number can presented so:
$$z = r e^{i p}$$
substitute to the equation
$$r^{4} e^{4 i p} = 256$$
where
$$r = 4$$
- the magnitude of the complex number
Substitute r:
$$e^{4 i p} = 1$$
Using Euler’s formula, we find roots for p
$$i \sin{\left(4 p \right)} + \cos{\left(4 p \right)} = 1$$
so
$$\cos{\left(4 p \right)} = 1$$
and
$$\sin{\left(4 p \right)} = 0$$
then
$$p = \frac{\pi N}{2}$$
where N=0,1,2,3,...
Looping through the values of N and substituting p into the formula for z
Consequently, the solution will be for z:
$$z_{1} = -4$$
$$z_{2} = 4$$
$$z_{3} = - 4 i$$
$$z_{4} = 4 i$$
do backward replacement
$$z = x$$
$$x = z$$
$$x_{1} = 4$$
$$x_{2} = -4$$
$$x_{1} = 4$$
$$x_{2} = -4$$
This roots
$$x_{2} = -4$$
$$x_{1} = 4$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{2}$$
For example, let's take the point
$$x_{0} = x_{2} - \frac{1}{10}$$
=
$$-4 + - \frac{1}{10}$$
=
$$- \frac{41}{10}$$
substitute to the expression
$$x^{4} > 256$$
$$\left(- \frac{41}{10}\right)^{4} > 256$$
one of the solutions of our inequality is:
$$x < -4$$
Other solutions will get with the changeover to the next point
etc.
The answer:
$$x < -4$$
$$x > 4$$
$$x^{4} > 256$$
To solve this inequality, we must first solve the corresponding equation:
$$x^{4} = 256$$
Solve:
Given the equation
$$x^{4} = 256$$
Because equation degree is equal to = 4 - contains the even number 4 in the numerator, then
the equation has two real roots.
Get the root 4-th degree of the equation sides:
We get:
$$\sqrt[4]{x^{4}} = \sqrt[4]{256}$$
$$\sqrt[4]{x^{4}} = \left(-1\right) \sqrt[4]{256}$$
or
$$x = 4$$
$$x = -4$$
We get the answer: x = 4
We get the answer: x = -4
or
$$x_{1} = -4$$
$$x_{2} = 4$$
All other 2 root(s) is the complex numbers.
do replacement:
$$z = x$$
then the equation will be the:
$$z^{4} = 256$$
Any complex number can presented so:
$$z = r e^{i p}$$
substitute to the equation
$$r^{4} e^{4 i p} = 256$$
where
$$r = 4$$
- the magnitude of the complex number
Substitute r:
$$e^{4 i p} = 1$$
Using Euler’s formula, we find roots for p
$$i \sin{\left(4 p \right)} + \cos{\left(4 p \right)} = 1$$
so
$$\cos{\left(4 p \right)} = 1$$
and
$$\sin{\left(4 p \right)} = 0$$
then
$$p = \frac{\pi N}{2}$$
where N=0,1,2,3,...
Looping through the values of N and substituting p into the formula for z
Consequently, the solution will be for z:
$$z_{1} = -4$$
$$z_{2} = 4$$
$$z_{3} = - 4 i$$
$$z_{4} = 4 i$$
do backward replacement
$$z = x$$
$$x = z$$
$$x_{1} = 4$$
$$x_{2} = -4$$
$$x_{1} = 4$$
$$x_{2} = -4$$
This roots
$$x_{2} = -4$$
$$x_{1} = 4$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{2}$$
For example, let's take the point
$$x_{0} = x_{2} - \frac{1}{10}$$
=
$$-4 + - \frac{1}{10}$$
=
$$- \frac{41}{10}$$
substitute to the expression
$$x^{4} > 256$$
$$\left(- \frac{41}{10}\right)^{4} > 256$$
2825761 ------- > 256 10000
one of the solutions of our inequality is:
$$x < -4$$
_____ _____
\ /
-------ο-------ο-------
x2 x1Other solutions will get with the changeover to the next point
etc.
The answer:
$$x < -4$$
$$x > 4$$
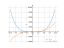
Solving inequality on a graph
Rapid solution
[src]
Or(And(-oo < x, x < -4), And(4 < x, x < oo))
$$\left(-\infty < x \wedge x < -4\right) \vee \left(4 < x \wedge x < \infty\right)$$
((-oo < x)∧(x < -4))∨((4 < x)∧(x < oo))
Rapid solution 2
[src]
(-oo, -4) U (4, oo)
$$x\ in\ \left(-\infty, -4\right) \cup \left(4, \infty\right)$$
x in Union(Interval.open(-oo, -4), Interval.open(4, oo))

 x⁴
x⁴
 x⁴
x⁴
 256
256