4*x+3>-8 inequation
The solution
Detail solution
Given the inequality:
$$4 x + 3 > -8$$
To solve this inequality, we must first solve the corresponding equation:
$$4 x + 3 = -8$$
Solve:
Given the linear equation:
Move free summands (without x)
from left part to right part, we given:
$$4 x = -11$$
Divide both parts of the equation by 4
$$x_{1} = - \frac{11}{4}$$
$$x_{1} = - \frac{11}{4}$$
This roots
$$x_{1} = - \frac{11}{4}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$- \frac{11}{4} + - \frac{1}{10}$$
=
$$- \frac{57}{20}$$
substitute to the expression
$$4 x + 3 > -8$$
$$\frac{\left(-57\right) 4}{20} + 3 > -8$$
Then
$$x < - \frac{11}{4}$$
no execute
the solution of our inequality is:
$$x > - \frac{11}{4}$$
$$4 x + 3 > -8$$
To solve this inequality, we must first solve the corresponding equation:
$$4 x + 3 = -8$$
Solve:
Given the linear equation:
4*x+3 = -8
Move free summands (without x)
from left part to right part, we given:
$$4 x = -11$$
Divide both parts of the equation by 4
x = -11 / (4)
$$x_{1} = - \frac{11}{4}$$
$$x_{1} = - \frac{11}{4}$$
This roots
$$x_{1} = - \frac{11}{4}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$- \frac{11}{4} + - \frac{1}{10}$$
=
$$- \frac{57}{20}$$
substitute to the expression
$$4 x + 3 > -8$$
$$\frac{\left(-57\right) 4}{20} + 3 > -8$$
-42/5 > -8
Then
$$x < - \frac{11}{4}$$
no execute
the solution of our inequality is:
$$x > - \frac{11}{4}$$
_____
/
-------ο-------
x1
Solving inequality on a graph
Rapid solution
[src]
And(-11/4 < x, x < oo)
$$- \frac{11}{4} < x \wedge x < \infty$$
(-11/4 < x)∧(x < oo)
Rapid solution 2
[src]
(-11/4, oo)
$$x\ in\ \left(- \frac{11}{4}, \infty\right)$$
x in Interval.open(-11/4, oo)

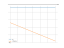 -8
-8
 4*x+3
4*x+3
 -8
-8