cos(2x)^2-sin(2x)^2<=sqrt(3)/2 inequation
The solution
You have entered
[src]
___
2 2 \/ 3
cos (2*x) - sin (2*x) <= -----
2
$$- \sin^{2}{\left(2 x \right)} + \cos^{2}{\left(2 x \right)} \leq \frac{\sqrt{3}}{2}$$
-sin(2*x)^2 + cos(2*x)^2 <= sqrt(3)/2
Detail solution
Given the inequality:
$$- \sin^{2}{\left(2 x \right)} + \cos^{2}{\left(2 x \right)} \leq \frac{\sqrt{3}}{2}$$
To solve this inequality, we must first solve the corresponding equation:
$$- \sin^{2}{\left(2 x \right)} + \cos^{2}{\left(2 x \right)} = \frac{\sqrt{3}}{2}$$
Solve:
Given the equation
$$- \sin^{2}{\left(2 x \right)} + \cos^{2}{\left(2 x \right)} = \frac{\sqrt{3}}{2}$$
transform
$$2 \cos^{2}{\left(2 x \right)} - 1 - \frac{\sqrt{3}}{2} = 0$$
$$2 \cos^{2}{\left(2 x \right)} - 1 - \frac{\sqrt{3}}{2} = 0$$
Do replacement
$$w = \cos{\left(2 x \right)}$$
This equation is of the form
$$a\ w^2 + b\ w + c = 0$$
A quadratic equation can be solved using the discriminant
The roots of the quadratic equation:
$$w_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where $D = b^2 - 4 a c$ is the discriminant.
Because
$$a = 2$$
$$b = 0$$
$$c = -1 - \frac{\sqrt{3}}{2}$$
, then
$$D = b^2 - 4\ a\ c = $$
$$0^{2} - 2 \cdot 4 \left(-1 - \frac{\sqrt{3}}{2}\right) = 4 \sqrt{3} + 8$$
Because D > 0, then the equation has two roots.
$$w_1 = \frac{(-b + \sqrt{D})}{2 a}$$
$$w_2 = \frac{(-b - \sqrt{D})}{2 a}$$
or
$$w_{1} = \frac{\sqrt{4 \sqrt{3} + 8}}{4}$$
Simplify
$$w_{2} = - \frac{\sqrt{4 \sqrt{3} + 8}}{4}$$
Simplify
do backward replacement
$$\cos{\left(2 x \right)} = w$$
$$\cos{\left(2 x \right)} = w$$
- this is the simplest trigonometric equation
This equation is transformed to
$$2 x = 2 \pi n + \operatorname{acos}{\left(w \right)}$$
$$2 x = 2 \pi n + \operatorname{acos}{\left(w \right)} - \pi$$
Or
$$2 x = 2 \pi n + \operatorname{acos}{\left(w \right)}$$
$$2 x = 2 \pi n + \operatorname{acos}{\left(w \right)} - \pi$$
, where n - is a integer
Divide both parts of the equation by
$$2$$
get the intermediate answer:
$$x = \pi n + \frac{\operatorname{acos}{\left(w \right)}}{2}$$
$$x = \pi n + \frac{\operatorname{acos}{\left(w \right)}}{2} - \frac{\pi}{2}$$
substitute w:
$$x_{1} = \pi n + \frac{\operatorname{acos}{\left(w_{1} \right)}}{2}$$
$$x_{1} = \pi n + \frac{\operatorname{acos}{\left(\frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{1} = \pi n + \frac{\operatorname{acos}{\left(\frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{2} = \pi n + \frac{\operatorname{acos}{\left(w_{2} \right)}}{2}$$
$$x_{2} = \pi n + \frac{\operatorname{acos}{\left(- \frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{2} = \pi n + \frac{\operatorname{acos}{\left(- \frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{3} = \pi n + \frac{\operatorname{acos}{\left(w_{1} \right)}}{2} - \frac{\pi}{2}$$
$$x_{3} = \pi n - \frac{\pi}{2} + \frac{\operatorname{acos}{\left(\frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{3} = \pi n - \frac{\pi}{2} + \frac{\operatorname{acos}{\left(\frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{4} = \pi n + \frac{\operatorname{acos}{\left(w_{2} \right)}}{2} - \frac{\pi}{2}$$
$$x_{4} = \pi n - \frac{\pi}{2} + \frac{\operatorname{acos}{\left(- \frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{4} = \pi n - \frac{\pi}{2} + \frac{\operatorname{acos}{\left(- \frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{1} = - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{2} = \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{3} = - \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{4} = \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{1} = - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{2} = \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{3} = - \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{4} = \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
This roots
$$x_{1} = - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{3} = - \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{4} = \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{2} = \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} \leq x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} - \frac{1}{10}$$
substitute to the expression
$$- \sin^{2}{\left(2 x \right)} + \cos^{2}{\left(2 x \right)} \leq \frac{\sqrt{3}}{2}$$
$$- \sin^{2}{\left(2 \left(- \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} - \frac{1}{10}\right) \right)} + \cos^{2}{\left(2 \left(- \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} - \frac{1}{10}\right) \right)} \leq \frac{\sqrt{3}}{2}$$
but
Then
$$x \leq - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
no execute
one of the solutions of our inequality is:
$$x \geq - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} \wedge x \leq - \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
Other solutions will get with the changeover to the next point
etc.
The answer:
$$x \geq - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} \wedge x \leq - \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x \geq \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)} \wedge x \leq \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$- \sin^{2}{\left(2 x \right)} + \cos^{2}{\left(2 x \right)} \leq \frac{\sqrt{3}}{2}$$
To solve this inequality, we must first solve the corresponding equation:
$$- \sin^{2}{\left(2 x \right)} + \cos^{2}{\left(2 x \right)} = \frac{\sqrt{3}}{2}$$
Solve:
Given the equation
$$- \sin^{2}{\left(2 x \right)} + \cos^{2}{\left(2 x \right)} = \frac{\sqrt{3}}{2}$$
transform
$$2 \cos^{2}{\left(2 x \right)} - 1 - \frac{\sqrt{3}}{2} = 0$$
$$2 \cos^{2}{\left(2 x \right)} - 1 - \frac{\sqrt{3}}{2} = 0$$
Do replacement
$$w = \cos{\left(2 x \right)}$$
This equation is of the form
$$a\ w^2 + b\ w + c = 0$$
A quadratic equation can be solved using the discriminant
The roots of the quadratic equation:
$$w_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where $D = b^2 - 4 a c$ is the discriminant.
Because
$$a = 2$$
$$b = 0$$
$$c = -1 - \frac{\sqrt{3}}{2}$$
, then
$$D = b^2 - 4\ a\ c = $$
$$0^{2} - 2 \cdot 4 \left(-1 - \frac{\sqrt{3}}{2}\right) = 4 \sqrt{3} + 8$$
Because D > 0, then the equation has two roots.
$$w_1 = \frac{(-b + \sqrt{D})}{2 a}$$
$$w_2 = \frac{(-b - \sqrt{D})}{2 a}$$
or
$$w_{1} = \frac{\sqrt{4 \sqrt{3} + 8}}{4}$$
Simplify
$$w_{2} = - \frac{\sqrt{4 \sqrt{3} + 8}}{4}$$
Simplify
do backward replacement
$$\cos{\left(2 x \right)} = w$$
$$\cos{\left(2 x \right)} = w$$
- this is the simplest trigonometric equation
This equation is transformed to
$$2 x = 2 \pi n + \operatorname{acos}{\left(w \right)}$$
$$2 x = 2 \pi n + \operatorname{acos}{\left(w \right)} - \pi$$
Or
$$2 x = 2 \pi n + \operatorname{acos}{\left(w \right)}$$
$$2 x = 2 \pi n + \operatorname{acos}{\left(w \right)} - \pi$$
, where n - is a integer
Divide both parts of the equation by
$$2$$
get the intermediate answer:
$$x = \pi n + \frac{\operatorname{acos}{\left(w \right)}}{2}$$
$$x = \pi n + \frac{\operatorname{acos}{\left(w \right)}}{2} - \frac{\pi}{2}$$
substitute w:
$$x_{1} = \pi n + \frac{\operatorname{acos}{\left(w_{1} \right)}}{2}$$
$$x_{1} = \pi n + \frac{\operatorname{acos}{\left(\frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{1} = \pi n + \frac{\operatorname{acos}{\left(\frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{2} = \pi n + \frac{\operatorname{acos}{\left(w_{2} \right)}}{2}$$
$$x_{2} = \pi n + \frac{\operatorname{acos}{\left(- \frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{2} = \pi n + \frac{\operatorname{acos}{\left(- \frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{3} = \pi n + \frac{\operatorname{acos}{\left(w_{1} \right)}}{2} - \frac{\pi}{2}$$
$$x_{3} = \pi n - \frac{\pi}{2} + \frac{\operatorname{acos}{\left(\frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{3} = \pi n - \frac{\pi}{2} + \frac{\operatorname{acos}{\left(\frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{4} = \pi n + \frac{\operatorname{acos}{\left(w_{2} \right)}}{2} - \frac{\pi}{2}$$
$$x_{4} = \pi n - \frac{\pi}{2} + \frac{\operatorname{acos}{\left(- \frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{4} = \pi n - \frac{\pi}{2} + \frac{\operatorname{acos}{\left(- \frac{\sqrt{4 \sqrt{3} + 8}}{4} \right)}}{2}$$
$$x_{1} = - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{2} = \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{3} = - \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{4} = \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{1} = - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{2} = \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{3} = - \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{4} = \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
This roots
$$x_{1} = - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{3} = - \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{4} = \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x_{2} = \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} \leq x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} - \frac{1}{10}$$
substitute to the expression
$$- \sin^{2}{\left(2 x \right)} + \cos^{2}{\left(2 x \right)} \leq \frac{\sqrt{3}}{2}$$
$$- \sin^{2}{\left(2 \left(- \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} - \frac{1}{10}\right) \right)} + \cos^{2}{\left(2 \left(- \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} - \frac{1}{10}\right) \right)} \leq \frac{\sqrt{3}}{2}$$
/ / ______________________________\\ / / ______________________________\\
| | / ___________ || | | / ___________ ||
| | / ___ / ___ || | | / ___ / ___ || ___
2|1 |\/ 6 + \/ 3 + 4*\/ 2 + \/ 3 || 2|1 |\/ 6 + \/ 3 + 4*\/ 2 + \/ 3 || \/ 3
cos |- + 2*atan|----------------------------------|| - sin |- + 2*atan|----------------------------------|| <= -----
|5 | ___________ || |5 | ___________ || 2
| | / ___ || | | / ___ ||
\ \ \/ 2 - \/ 3 // \ \ \/ 2 - \/ 3 //
but
/ / ______________________________\\ / / ______________________________\\
| | / ___________ || | | / ___________ ||
| | / ___ / ___ || | | / ___ / ___ || ___
2|1 |\/ 6 + \/ 3 + 4*\/ 2 + \/ 3 || 2|1 |\/ 6 + \/ 3 + 4*\/ 2 + \/ 3 || \/ 3
cos |- + 2*atan|----------------------------------|| - sin |- + 2*atan|----------------------------------|| >= -----
|5 | ___________ || |5 | ___________ || 2
| | / ___ || | | / ___ ||
\ \ \/ 2 - \/ 3 // \ \ \/ 2 - \/ 3 //
Then
$$x \leq - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
no execute
one of the solutions of our inequality is:
$$x \geq - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} \wedge x \leq - \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
_____ _____
/ \ / \
-------•-------•-------•-------•-------
x_1 x_3 x_4 x_2Other solutions will get with the changeover to the next point
etc.
The answer:
$$x \geq - \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)} \wedge x \leq - \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
$$x \geq \operatorname{atan}{\left(\frac{\sqrt{- 4 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 6}}{\sqrt{- \sqrt{3} + 2}} \right)} \wedge x \leq \operatorname{atan}{\left(\frac{\sqrt{\sqrt{3} + 6 + 4 \sqrt{\sqrt{3} + 2}}}{\sqrt{- \sqrt{3} + 2}} \right)}$$
Solving inequality on a graph
Rapid solution
[src]
/ / / ___ ___\ / ___ ___\ \ / / ___ ___\ / ___ ___\ \\ | | |\/ 2 - \/ 6 | |\/ 2 - \/ 6 | | | |\/ 2 - \/ 6 | |\/ 2 - \/ 6 | || | | atan|-------------| atan|-------------| | | atan|-------------| -atan|-------------| || | | | ___ ___| | ___ ___| | | | ___ ___| | ___ ___| || | | \\/ 2 + \/ 6 / pi \\/ 2 + \/ 6 / | | pi \\/ 2 + \/ 6 / \\/ 2 + \/ 6 / || Or|And|x <= pi + -------------------, -- - ------------------- <= x|, And|x <= -- + -------------------, --------------------- <= x|| \ \ 2 2 2 / \ 2 2 2 //
$$\left(x \leq \frac{\operatorname{atan}{\left(\frac{- \sqrt{6} + \sqrt{2}}{\sqrt{2} + \sqrt{6}} \right)}}{2} + \pi \wedge - \frac{\operatorname{atan}{\left(\frac{- \sqrt{6} + \sqrt{2}}{\sqrt{2} + \sqrt{6}} \right)}}{2} + \frac{\pi}{2} \leq x\right) \vee \left(x \leq \frac{\operatorname{atan}{\left(\frac{- \sqrt{6} + \sqrt{2}}{\sqrt{2} + \sqrt{6}} \right)}}{2} + \frac{\pi}{2} \wedge - \frac{\operatorname{atan}{\left(\frac{- \sqrt{6} + \sqrt{2}}{\sqrt{2} + \sqrt{6}} \right)}}{2} \leq x\right)$$
((-atan((sqrt(2) - sqrt(6))/(sqrt(2) + sqrt(6)))/2 <= x)∧(x <= pi/2 + atan((sqrt(2) - sqrt(6))/(sqrt(2) + sqrt(6)))/2))∨((x <= pi + atan((sqrt(2) - sqrt(6))/(sqrt(2) + sqrt(6)))/2)∧(pi/2 - atan((sqrt(2) - sqrt(6))/(sqrt(2) + sqrt(6)))/2 <= x))
Rapid solution 2
[src]
/ ___ ___\ / ___ ___\ / ___ ___\ / ___ ___\
|\/ 2 - \/ 6 | |\/ 2 - \/ 6 | |\/ 2 - \/ 6 | |\/ 2 - \/ 6 |
-atan|-------------| atan|-------------| atan|-------------| atan|-------------|
| ___ ___| | ___ ___| | ___ ___| | ___ ___|
\\/ 2 + \/ 6 / pi \\/ 2 + \/ 6 / pi \\/ 2 + \/ 6 / \\/ 2 + \/ 6 /
[---------------------, -- + -------------------] U [-- - -------------------, pi + -------------------]
2 2 2 2 2 2
$$x\ in\ \left[- \frac{\operatorname{atan}{\left(\frac{- \sqrt{6} + \sqrt{2}}{\sqrt{2} + \sqrt{6}} \right)}}{2}, \frac{\operatorname{atan}{\left(\frac{- \sqrt{6} + \sqrt{2}}{\sqrt{2} + \sqrt{6}} \right)}}{2} + \frac{\pi}{2}\right] \cup \left[- \frac{\operatorname{atan}{\left(\frac{- \sqrt{6} + \sqrt{2}}{\sqrt{2} + \sqrt{6}} \right)}}{2} + \frac{\pi}{2}, \frac{\operatorname{atan}{\left(\frac{- \sqrt{6} + \sqrt{2}}{\sqrt{2} + \sqrt{6}} \right)}}{2} + \pi\right]$$
x in Union(Interval(-atan((-sqrt(6) + sqrt(2))/(sqrt(2) + sqrt(6)))/2 + pi/2, atan((-sqrt(6) + sqrt(2))/(sqrt(2) + sqrt(6)))/2 + pi), Interval(-atan((-sqrt(6) + sqrt(2))/(sqrt(2) + sqrt(6)))/2, atan((-sqrt(6) + sqrt(2))/(sqrt(2) + sqrt(6)))/2 + pi/2))
The graph
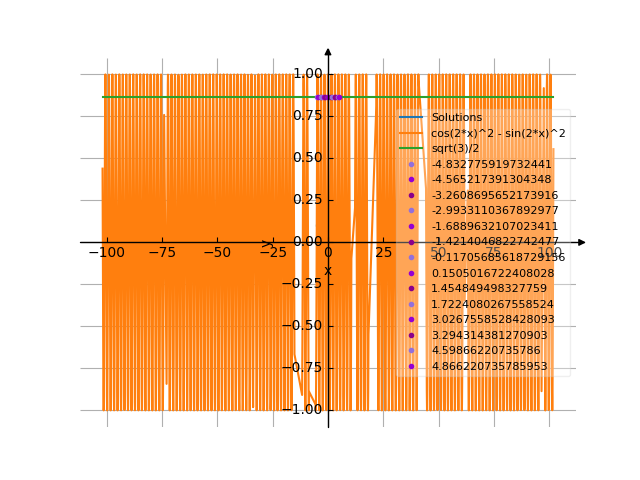

![Solve the inequality cos(2x)²-sin(2x)²<=sqrt(3)/2 (co sinus of e of (2x) squared minus sinus of (2x) squared less than or equal to square root of (3) divide by 2) - Specify the set of solutions of the inequality in detail step by step. [THERE'S THE ANSWER!] cos(2x)^2-sin(2x)^2<=sqrt(3)/2](/media/krcore-image-pods/176/hash/inequation/1/12/d3d18d24c665ee382c1d358bad211.png)