Mister Exam

Other calculators

2^x=16^2

2^x=16^2 equation

The teacher will be very surprised to see your correct solution 😉

v

Numerical solution:

Do search numerical solution at [, ]

The solution

You have entered [src] 
 x     2
2  = 16
2x=1622^{x} = 16^{2}
Simplify
Detail solution
Given the equation:
2x=1622^{x} = 16^{2}
or
2x−162=02^{x} - 16^{2} = 0
or
2x=2562^{x} = 256
or
2x=2562^{x} = 256
- this is the simplest exponential equation
Do replacement
v=2xv = 2^{x}
we get
v−256=0v - 256 = 0
or
v−256=0v - 256 = 0
Move free summands (without v)
from left part to right part, we given:
v=256v = 256
We get the answer: v = 256
do backward replacement
2x=v2^{x} = v
or
x=log⁡(v)log⁡(2)x = \frac{\log{\left(v \right)}}{\log{\left(2 \right)}}
The final answer
x1=log⁡(256)log⁡(2)=8x_{1} = \frac{\log{\left(256 \right)}}{\log{\left(2 \right)}} = 8
The graph
-2.50.02.55.07.510.012.515.017.520.022.525.00500
Plot the graph f1(x)
Plot the graph f2(x)
Sum and product of roots [src] 
sum
8
(8)\left(8\right) 
=
8
88
Simplify 
product
8
(8)\left(8\right) 
=
8
88
Simplify
Rapid solution [src] 
x_1 = 8
x1=8x_{1} = 8
Simplify
Numerical answer [src] 
x1 = 8.0
x1 = 8.0
The graph
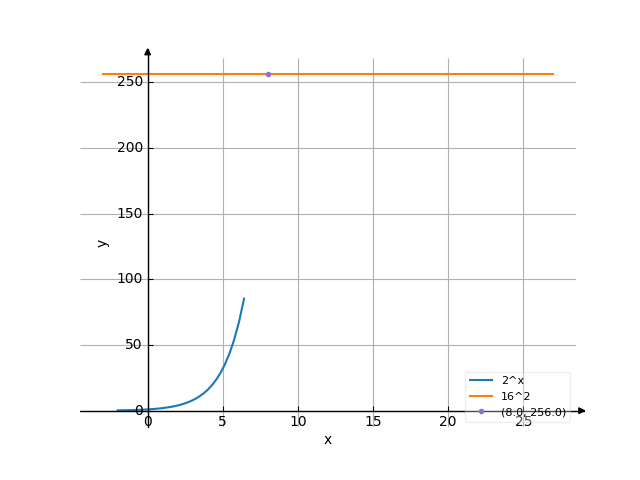
2^x=16^2 equation
    © Mister Exam – Calculator