(3/2)^x=16/81 equation
The teacher will be very surprised to see your correct solution 😉
The solution
Detail solution
Given the equation:
$$\left(\frac{3}{2}\right)^{x} = \frac{16}{81}$$
or
$$\left(\frac{3}{2}\right)^{x} - \frac{16}{81} = 0$$
or
$$\left(\frac{3}{2}\right)^{x} = \frac{16}{81}$$
or
$$\left(\frac{3}{2}\right)^{x} = \frac{16}{81}$$
- this is the simplest exponential equation
Do replacement
$$v = \left(\frac{3}{2}\right)^{x}$$
we get
$$v - \frac{16}{81} = 0$$
or
$$v - \frac{16}{81} = 0$$
Move free summands (without v)
from left part to right part, we given:
$$v = \frac{16}{81}$$
We get the answer: v = 16/81
do backward replacement
$$\left(\frac{3}{2}\right)^{x} = v$$
or
$$x = \frac{\log{\left(v \right)}}{\log{\left(\frac{3}{2} \right)}}$$
The final answer
$$x_{1} = \frac{\log{\left(\frac{16}{81} \right)}}{\log{\left(\frac{3}{2} \right)}} = -4$$
$$\left(\frac{3}{2}\right)^{x} = \frac{16}{81}$$
or
$$\left(\frac{3}{2}\right)^{x} - \frac{16}{81} = 0$$
or
$$\left(\frac{3}{2}\right)^{x} = \frac{16}{81}$$
or
$$\left(\frac{3}{2}\right)^{x} = \frac{16}{81}$$
- this is the simplest exponential equation
Do replacement
$$v = \left(\frac{3}{2}\right)^{x}$$
we get
$$v - \frac{16}{81} = 0$$
or
$$v - \frac{16}{81} = 0$$
Move free summands (without v)
from left part to right part, we given:
$$v = \frac{16}{81}$$
We get the answer: v = 16/81
do backward replacement
$$\left(\frac{3}{2}\right)^{x} = v$$
or
$$x = \frac{\log{\left(v \right)}}{\log{\left(\frac{3}{2} \right)}}$$
The final answer
$$x_{1} = \frac{\log{\left(\frac{16}{81} \right)}}{\log{\left(\frac{3}{2} \right)}} = -4$$
Sum and product of roots
[src]
sum
0 - 4
$$-4 + 0$$
=
-4
$$-4$$
product
1*-4
$$1 \left(-4\right)$$
=
-4
$$-4$$
-4
The graph
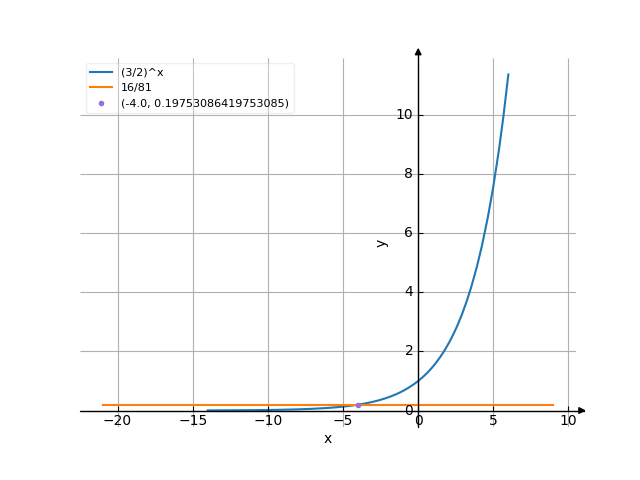

![Solve the equation (3/2)^x=16/81 ((3 divide by 2) to the power of x equally 16 divide by 81) - Find the roots of the equation in detail step by step. [THERE'S THE ANSWER!] (3/2)^x=16/81](/media/krcore-image-pods/176/hash/equation/3/77/0039551fbce5c4cc02e82cfe107f0.png)
 Equation 4(5x+2)=10(2x-3)+15
Equation 4(5x+2)=10(2x-3)+15
 Equation x^2-4x+4=0
Equation x^2-4x+4=0
 Equation x^2+3x=0
Equation x^2+3x=0
 Equation x^2+4x-5=0
Equation x^2+4x-5=0
 (3/2)^x
(3/2)^x