sqrt(2*cos(x))-1=0 equation
The teacher will be very surprised to see your correct solution 😉
The solution
Detail solution
Given the equation
transform
Do replacement
Given the equation
Because equation degree is equal to = 1/2 - does not contain even numbers in the numerator, then
the equation has single real root.
We raise the equation sides to 2-th degree:
We get:
or
Divide both parts of the equation by 2
We get the answer: w = 1/2
The final answer:
do backward replacement
- this is the simplest trigonometric equation
This equation is transformed to
Or
, where n - is a integer
substitute w:
transform
Do replacement
Given the equation
Because equation degree is equal to = 1/2 - does not contain even numbers in the numerator, then
the equation has single real root.
We raise the equation sides to 2-th degree:
We get:
or
Divide both parts of the equation by 2
w = 1 / (2)
We get the answer: w = 1/2
The final answer:
do backward replacement
- this is the simplest trigonometric equation
This equation is transformed to
Or
, where n - is a integer
substitute w:
Sum and product of roots
[src]
sum
pi 5*pi -- + ---- 3 3
=
2*pi
product
pi 5*pi -- * ---- 3 3
=
2 5*pi ----- 9
Numerical answer
[src]
x1 = -76.4454212373516
x2 = 76.4454212373516
x3 = -61.7846555205993
x4 = 11.5191730631626
x5 = -86.9173967493176
x6 = -51.3126800086333
x7 = -26.1799387799149
x8 = 70.162235930172
x9 = 68.0678408277789
x10 = -57.5958653158129
x11 = 45.0294947014537
x12 = -55.5014702134197
x13 = -68.0678408277789
x14 = 19.8967534727354
x15 = -93.2005820564972
x16 = 32.4631240870945
x17 = 49.2182849062401
x18 = 74.3510261349584
x19 = -7.33038285837618
x20 = -70.162235930172
x21 = 5.23598775598299
x22 = -42.9350995990605
x23 = 17.8023583703422
x24 = -11.5191730631626
x25 = -45.0294947014537
x26 = 7.33038285837618
x27 = -30.3687289847013
x28 = 63.8790506229925
x29 = -74.3510261349584
x30 = -99.4837673636768
x31 = 26.1799387799149
x32 = -89.0117918517108
x33 = 95.2949771588904
x34 = 24.0855436775217
x35 = -13.6135681655558
x36 = -24.0855436775217
x37 = 51.3126800086333
x38 = -49.2182849062401
x39 = 57.5958653158129
x40 = 61.7846555205993
x41 = 38.7463093942741
x42 = 55.5014702134197
x43 = 99.4837673636768
x44 = -5.23598775598299
x45 = -63.8790506229925
x46 = 82.7286065445312
x47 = -1.0471975511966
x48 = -32.4631240870945
x49 = -82.7286065445312
x50 = -19.8967534727354
x51 = -36.6519142918809
x52 = 89.0117918517108
x53 = -80.634211442138
x54 = 80.634211442138
x55 = -9275.02871094827
x56 = 1.0471975511966
x57 = 86.9173967493176
x58 = -38.7463093942741
x59 = 36.6519142918809
x60 = 13.6135681655558
x61 = 42.9350995990605
x62 = 30.3687289847013
x63 = 93.2005820564972
x64 = -95.2949771588904
x65 = -17.8023583703422
x65 = -17.8023583703422
The graph
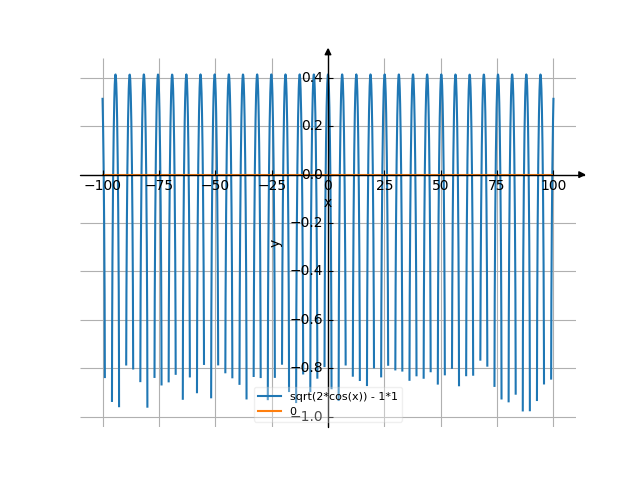

![Solve the equation sqrt(2*cos(x))-1=0 (square root of (2 multiply by co sinus of e of (x)) minus 1 equally 0) - Find the roots of the equation in detail step by step. [THERE'S THE ANSWER!] sqrt(2*cos(x))-1=0](/media/krcore-image-pods/176/hash/equation/f/b3/52272a15c61e0cf3eaeb3f44f020c.png)
 Equation 1/(x-1)^2+4/(x-1)-12=0
Equation 1/(x-1)^2+4/(x-1)-12=0
 Equation 2sinxcos3x+sin4x=0
Equation 2sinxcos3x+sin4x=0