cos(x)=2 equation
The teacher will be very surprised to see your correct solution 😉
The solution
Detail solution
Given the equation
$$\cos{\left(x \right)} = 2$$
- this is the simplest trigonometric equation
As right part of the equation
modulo =
but cos
can no be more than 1 or less than -1
so the solution of the equation d'not exist.
$$\cos{\left(x \right)} = 2$$
- this is the simplest trigonometric equation
As right part of the equation
modulo =
True
but cos
can no be more than 1 or less than -1
so the solution of the equation d'not exist.
Rapid solution
[src]
x1 = 2*pi - I*im(acos(2))
$$x_{1} = 2 \pi - i \operatorname{im}{\left(\operatorname{acos}{\left(2 \right)}\right)}$$
x2 = I*im(acos(2)) + re(acos(2))
$$x_{2} = \operatorname{re}{\left(\operatorname{acos}{\left(2 \right)}\right)} + i \operatorname{im}{\left(\operatorname{acos}{\left(2 \right)}\right)}$$
Sum and product of roots
[src]
sum
0 + 2*pi - I*im(acos(2)) + I*im(acos(2)) + re(acos(2))
$$\left(0 + \left(2 \pi - i \operatorname{im}{\left(\operatorname{acos}{\left(2 \right)}\right)}\right)\right) + \left(\operatorname{re}{\left(\operatorname{acos}{\left(2 \right)}\right)} + i \operatorname{im}{\left(\operatorname{acos}{\left(2 \right)}\right)}\right)$$
=
2*pi + re(acos(2))
$$\operatorname{re}{\left(\operatorname{acos}{\left(2 \right)}\right)} + 2 \pi$$
product
1*(2*pi - I*im(acos(2)))*(I*im(acos(2)) + re(acos(2)))
$$1 \cdot \left(2 \pi - i \operatorname{im}{\left(\operatorname{acos}{\left(2 \right)}\right)}\right) \left(\operatorname{re}{\left(\operatorname{acos}{\left(2 \right)}\right)} + i \operatorname{im}{\left(\operatorname{acos}{\left(2 \right)}\right)}\right)$$
=
(2*pi - I*im(acos(2)))*(I*im(acos(2)) + re(acos(2)))
$$\left(2 \pi - i \operatorname{im}{\left(\operatorname{acos}{\left(2 \right)}\right)}\right) \left(\operatorname{re}{\left(\operatorname{acos}{\left(2 \right)}\right)} + i \operatorname{im}{\left(\operatorname{acos}{\left(2 \right)}\right)}\right)$$
(2*pi - i*im(acos(2)))*(i*im(acos(2)) + re(acos(2)))
Numerical answer
[src]
x1 = 6.28318530717959 - 1.31695789692482*i
x2 = 1.31695789692482*i
x2 = 1.31695789692482*i
The graph


![Solve the equation cos(x)=2 (co sinus of e of (x) equally 2) - Find the roots of the equation in detail step by step. [THERE'S THE ANSWER!] cos(x)=2](/media/krcore-image-pods/176/hash/equation/5/3c/4e21acc3c6183dc5f0a3b8020582e.png)
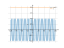 Equation cos(x)=2
Equation cos(x)=2
 Equation tg(x)=0
Equation tg(x)=0
 cos(x)
cos(x)
 cos(x)
cos(x)
 cos(x)
cos(x)