Mister Exam
Other calculators
- Derivative of a implicit defined function
- Derivative of Parametric Function
- Partial derivative of the function
- Curve tracing functions Step by Step
- Integral Step by Step
- Differential equations Step by Step
- Limits Step by Step
-
How to use it?
- Derivative of:
-
Derivative of 6
-
Derivative of x*e^x^2
-
Derivative of (x+4)^2*(x+1)+9
-
Derivative of (x+3)/(x-1)
-
Identical expressions
- y=xchx-x^2chx
- y equally xchx minus x squared chx
- y=xchx-x2chx
- y=xchx-x²chx
- y=xchx-x to the power of 2chx
-
Similar expressions
- y=xchx+x^2chx
Derivative of y=xchx-x^2chx
The solution
You have entered
[src]
2 x*cosh(x) - x *cosh(x)
$$- x^{2} \cosh{\left(x \right)} + x \cosh{\left(x \right)}$$
x*cosh(x) - x^2*cosh(x)
The first derivative
[src]
2 x*sinh(x) - x *sinh(x) - 2*x*cosh(x) + cosh(x)
$$- x^{2} \sinh{\left(x \right)} + x \sinh{\left(x \right)} - 2 x \cosh{\left(x \right)} + \cosh{\left(x \right)}$$
The second derivative
[src]
2 -2*cosh(x) + 2*sinh(x) + x*cosh(x) - x *cosh(x) - 4*x*sinh(x)
$$- x^{2} \cosh{\left(x \right)} - 4 x \sinh{\left(x \right)} + x \cosh{\left(x \right)} + 2 \sinh{\left(x \right)} - 2 \cosh{\left(x \right)}$$
The third derivative
[src]
2 -6*sinh(x) + 3*cosh(x) + x*sinh(x) - x *sinh(x) - 6*x*cosh(x)
$$- x^{2} \sinh{\left(x \right)} + x \sinh{\left(x \right)} - 6 x \cosh{\left(x \right)} - 6 \sinh{\left(x \right)} + 3 \cosh{\left(x \right)}$$
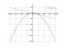
The graph