Mister Exam

Lang:

The derivative of the function/ y=x⁸/x²

You entered:

y=x⁸/x²

What you mean?

x^8/(x^2)

x^((8/x)^2)

x^((8/x)^2)

Derivative of y=x⁸/x²

The solution

You have entered [src]

 8
x 
--
 2
x

$$\frac{x^{8}}{x^{2}}$$

  / 8\
d |x |
--|--|
dx| 2|
  \x /

$$\frac{d}{d x} \frac{x^{8}}{x^{2}}$$

Transform

Detail solution

Apply the quotient rule, which is:

$\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}$

$f{\left(x \right)} = x^{8}$ and $g{\left(x \right)} = x^{2}$ .

To find $\frac{d}{d x} f{\left(x \right)}$ :
1. Apply the power rule: $x^{8}$ goes to $8 x^{7}$
To find $\frac{d}{d x} g{\left(x \right)}$ :
1. Apply the power rule: $x^{2}$ goes to $2 x$
Now plug in to the quotient rule:

$6 x^{5}$

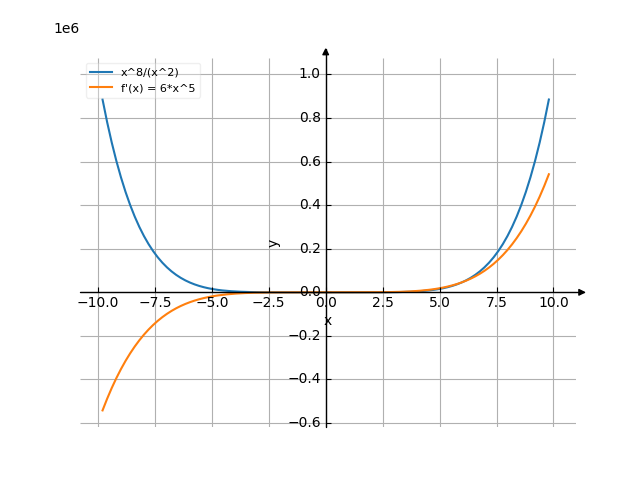
The answer is:

$6 x^{5}$

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

            7
     5   8*x 
- 2*x  + ----
           2 
          x

$$\frac{8 x^{7}}{x^{2}} - 2 x^{5}$$

Simplify

The second derivative [src]

    4
30*x

$$30 x^{4}$$

Simplify

The third derivative [src]

     3
120*x

$$120 x^{3}$$

Simplify

The graph

Derivative of y=x⁸/x²